Der Satz des Pythagoras: Ein Beweis durch Symmetrie
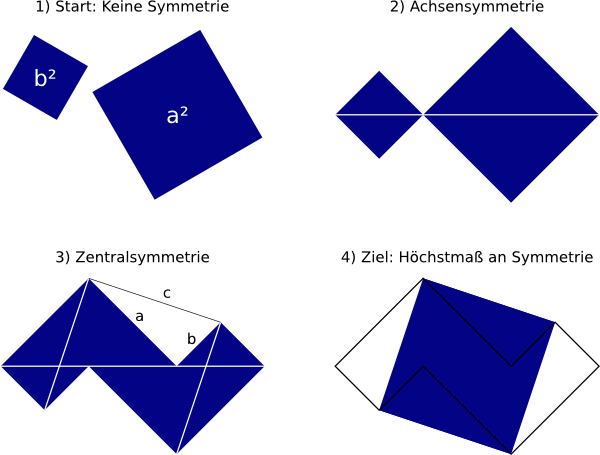
„Die Geometrie war bekanntlich die erste deduktive Wissenschaft, und diese Leitfunktion hat sie bis heute erhalten: Etwas more geometrico zu begründen, gilt überall als wirklich stichhaltige Argumentation. Deduktive Ordnung zwischen Aussagen zu entdecken und auszudrücken, ist hier das allgemeinbildende Ziel, das sicher nicht dann schon als erreicht angesehen werden kann, wenn in der Klasse Beweisrituale vorgeführt werden. Wie auch die Geschichte lehrt, kann Deduktivität in der Geometrie (und dann auch in anderen Bereichen) nur erfahren werden, wenn sie von einer kreativen Konstruktivität getragen und von der Suche nach Symmetrien und Asymmetrien geleitet wird. Ein Paradefall ist der Satz des Pythagoras, der in operativer Sprache lautet: Wenn mir zwei Quadrate mit den Seitenlängen a und b vorgelegt werden, so kann ich stets ein drittes Quadrat mit der Seitenlänge c konstruieren, so dass für die Flächeninhalte a² + b² = c² gilt. Dieser Satz motiviert sich nicht ohne weiteres durch das Anblicken rechtwinkliger Dreiecke, und seine Richtigkeit erschließt sich nicht dem blanken Augenschein. Es bedarf umstrukturierender Denkschritte (des Sehens mit den Augen des Geistes, wie Platon sagt). Eine der vielen Möglichkeiten deutet diese Figurenfolge an. Die umformenden Denkschritte können hier sogar durch ganz praktische Handlungen realisiert werden.
Von allgemeinbildendem Wert ist die Erfahrung, wie über Umorganisation einer Konfiguration, verbunden mit begrifflichen Absicherungen, eine neue Konfiguration entsteht, so dass die Wahrheit der Behauptung unbezweifelbar erkennbar wird, und gegen jeden Einwand verteidigt werden kann.“ (Winter, Heinrich 1995: Mathematikunterricht und Allgemeinbildung. In: GDM Mitteilungen, Heft 61 (1995), S. 37-46.)