Für eine korrekte Darstellung dieser Seite benötigen Sie einen XHTML-standardkonformen Browser, der die Darstellung von CSS-Dateien zulässt.

Inverse Gravimetric Problem

 
The inverse gravimetric problem consists of the reconstruction of the Earth's mass density distribution from measurements of the gravitational field. Based on Newton's Laws of Gravitation the gravitational potential V is given by a mass density distribution ρ as follows:

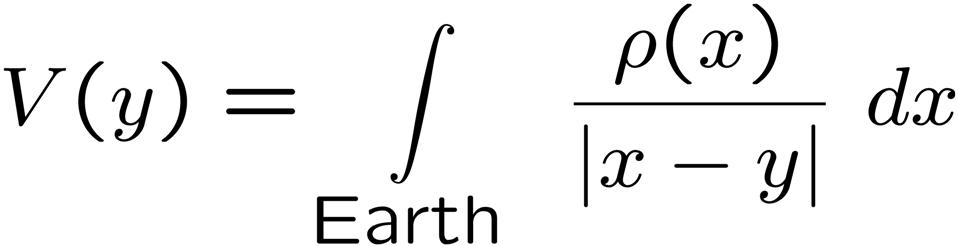
In reality, modern satellite missions such as CHAMP, GRACE, and GOCE allow a determination of the gravitational field with a rather good global coverage and high precision. From these data, a model of the gravitational potential V can be determined for the Earth whereas ρ is unknown. This means that the relation of the above equation has to be inverted. Problems of such kind are called inverse problems. According to Hadamard, an inverse problem is called well-posed if each of the following three criteria is satisfied:

  • a solution exists,
  • the solution is unique,
  • the solution is stable, i.e. it continuously depends on the given data (here: V).

Otherwise, the problem is called ill-posed. For such linear problems, the alternative definition by Nashed can be used: a problem is called well-posed if the image of the corresponding operator is not closed.

In case of the inverse gravimetric problem the following facts hold:

  • Existence: A solution is not given for every right hand side V. More precisely, for the solvability, V has to be harmonic outside the Earth, i.e. it has to satisfy a certain partial differential equation called the Laplace equation, and additionally it must satisfy the so-called Picard condition.
  • Uniqueness: It is well-known that the density cannot be uniquely recovered from the gravitational potential. To be more specific, only the harmonic part of the density function can uniquely be reconstructed, whereas the (in the sense of the L2-space) orthogonal, so-called anharmonic, part has the potential 0 and, therefore, does not leave any trace in the gravitational measurements. This non-uniqueness is a serious difficulty since the space of all anharmonic functions is infinite-dimensional. More precisely, its restriction to polynomials of degree < n+1 has a dimension which is cubic with respect to n, whereas the dimension of all harmonic polynomials of degree < n+1 is (n+1)2. Further details on the problem of non-uniqueness and associated historical aspects can be found in the survey article [2].
  • Stability: The density does not continuously depend on the gravitational potential. Moreover, a decomposition V^(n,j) of the potential V with respect to certain polynomial basis functions Yn,j, where n is the degree, (the spherical harmonics) shows that there is a relation (ρharm)^(n,j) = (T^(n))-1 V^(n,j) for the corresponding coefficients of the harmonic density ρharm. In case of satellite data, the only global type of gravitational data, this factor (T^(n))-1 exponentially diverges as n goes to infinity.

Hence, the gravimetry problem is ill-posed. Due to the exponential character of the instability, the inverse gravimetric problem in case of satellite data is called exponentially ill-posed.

For the (unique) recovery of the harmonic density function, a regularization method is required. The idea of such a regularization is that a sequence of approximations FJ to the exact solution ρharm  is calculated where each FJ continuously depends on V and the sequence converges to ρharm. In [1], a multiresolution regularization method is introduced, where FJ is calculated via a (spherical) convolution of an appropriate scaling function ΦJ with the given data function F

 


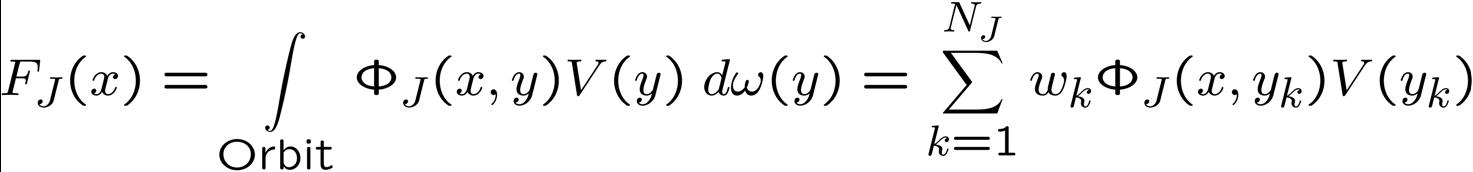
where these convolutions can be discretized with appropriate methods, as indicated. A scaling function ΦJ is, for instance, representable as a series of Legendre polynomials which can easily be calculated approximately via the Clenshaw algorithm. The recovered harmonic density in the Earth's crust at scale 10 for a certain choice of a scaling function (Gauß-Weierstraß scaling function) is illustrated below:
 

 


Here, gravitational data obtained from Satellite Gravity Gradiometry (SGG) were simulated at a 200 km orbit for the satellite mission GOCE. Further details on the theory and the numerics of the developed method can be found in [1].

 

[1] V. Michel: Regularized wavelet-based multiresolution recovery of the harmonic mass density distribution from data of the earth's gravitational field at satellite height, Inverse Problems, 21 (2005), 997-1025 .

[2] V. Michel, A.S. Fokas: A unified approach to various techniques for the non-uniqueness of the inverse gravimetric problem and wavelet-based methods, Inverse Problems, 24 (2008), 045019 (25pp) .