Galerie

Modell- und Netzadaptivität

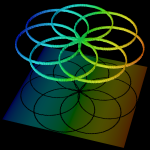	Schwache 2D-3D-Kopplung Nahe den Kreislinien wird auf einem dreidimensionalen Netz gerechnet, ansonsten auf einem zweidimensionalen. Die Kopplungsbedingung wird schwach formuliert, so daß für die Ansatzfunktionen im 2D- und 3D-Bereich Polynome verschiedener Ordnung gewählt werden können. Gelöst wird das Wärmeleitungsproblem. Weiter...
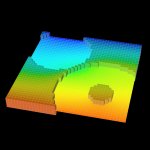	Diskrete 2D-3D-Kopplung Die 2D-3D-Kopplung erfolgt am diskreten System.
	Elastoplastizität kleiner Verformungen Dargestellt ist die plastische Verfestigung. Das Netz wird adaptiv verfeinert.
	Rißausbreitung Die Risse breiten sich im Laufe der Rechnung aus. Das Netz wird nach einem Spannungskriterium aufgetrennt. Weiter...
	Rißausbreitung mit lokaler Netzverfeinerung Am Riß wird das Netz lokal verfeinert. Der Riß breitet sich nach einem Spannungskriterium aus. Der kurvenförmige Verlauf wird durch festere kreisförmige Einschlüsse im Material verursacht. Weiter...

Kontakt und Reibung

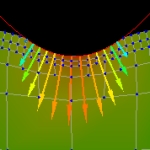	2D-Kontaktproblem auf periodischen Gebieten Wenn gewellte Oberflächen aufeinanderreiben, so kann es ausreichend sein, nur wenige Perioden zu betrachten. Weiter...
	3D-Kontaktproblem auf periodischen Gebieten Ein Zylinder dient als Beispiel für ein Kontaktproblem im Dreidimensionalen. Die Stirnseiten erhalten periodische Randbedingungen. Weiter...
	Reibungsfreier Kontakt (Signorini-Problem) Ein Zylinder wird durch das äußere Hindernis zusammengedrückt.
	Kontakt mit Coulomb-Reibung Die Coulomb-Reibung beschreibt das Haften und Gleiten im Kontaktbereich. Überschreiten die Reibkräfte einen Grenzwert, so beginnen die Kontaktflächen gegeneinander zu gleiten.
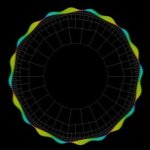	Geschmierte Reibung In dem farbigen gewellten Spalt befindet sich eine Flüssigkeit. Die Spaltströmung wird mit der Reynoldsgleichung modelliert.

Umformvorgänge und Theorie großer Verformungen

	Funktion der Inneren Energie Funktion der Energie für ein Elastizitätsmodell.
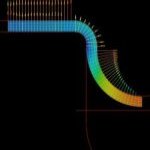	Elastizität großer Verformungen Bei großen Verformungen verliert die lineare Theorie ihre Gültigkeit.
	Elastizität und Elastoplastizität großer Verformungen Aus einer Platte wird ein Napf geformt. Aufgrund der Symmetrie braucht nur ein Viertel berechnet zu werden. Auf den Schnittflächen sind entsprechende Symmetrierandbedingungen gegeben. Das Material ist elastisch. Deshalb geht die Verformung vollständig zurück, wenn sich der Stempel hebt. Weiter...
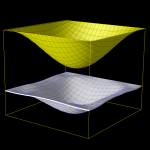	Elastoplastizität großer Verformungen Dargestellt ist ein Umformvorgang. Die gelbe Form ist der Stempel, das Weiße das Blech nach der Rückfederung.

Danksagung

Die Computerprogramme, die hinter diesen Bildern stecken, beruhen auf der C++-Programmbibliothek deal.II (www.dealii.org), deren Entwicklern für die Vorarbeit herzlich gedankt sei.