P4: Aspekte eines empirisch-gegenständlichen Mathematikunterrichts im Kontext digitaler Medien
Mitarbeiter:innen: Dr. Frederik Dilling, Dr. Felicitas Pielsticker, Rebecca Schneider, Amelie Vogler, Prof. Dr. Ingo Witzke
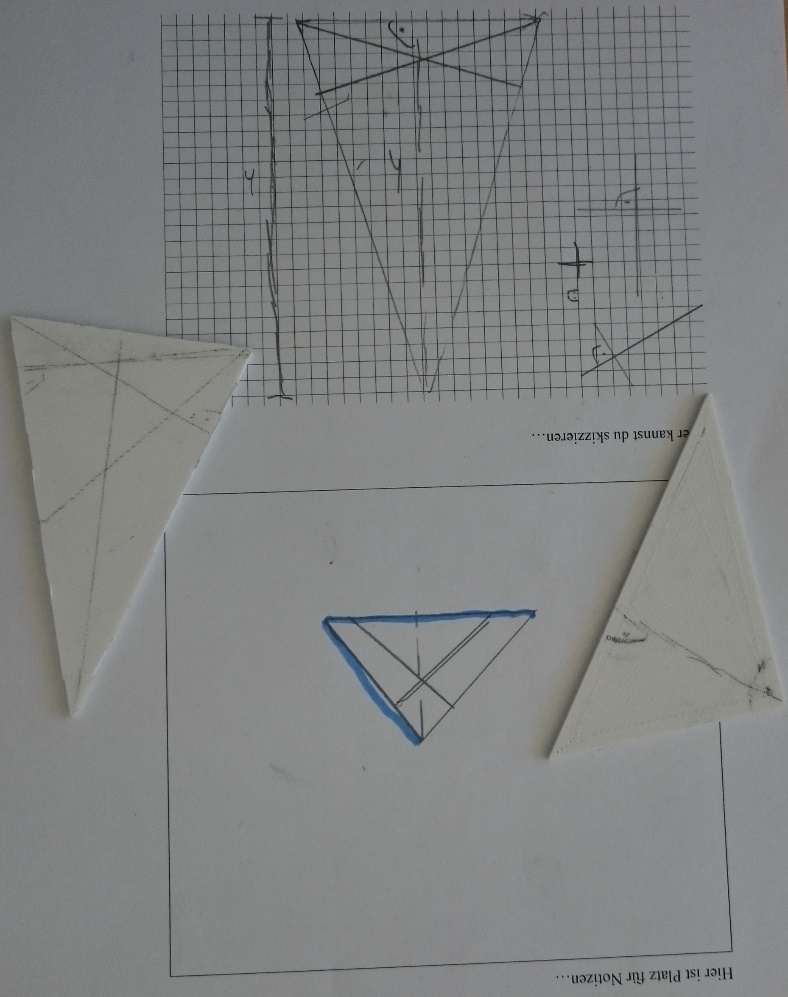
Der Mathematikunterricht in der Schule ist aus lern- und bildungstheoretischen Gründen von Anschaulichkeit und Realitätsbezug geprägt (vgl. Hefendehl-Hebeker, 2016). Mathematisches Wissen wird dabei von den Schüler:innen nicht nur zur Beschreibung empirischer Objekte (zum Beispiel Zeichenblattfiguren) angewendet, sondern auch auf der Grundlage dieser Objekte entwickelt. Begründet durch die Ergebnisse mehrere Studien (vgl. zum Beispiel Witzke, 2009; Schlicht, 2016; Schiffer, 2019; Pielsticker, 2020; Stoffels, 2020, Dilling, 2021) kann mittlerweile davon ausgegangen werden, dass Schüler:innen Mathematik in einem solchen empirisch-gegenständlich geprägten Unterricht nicht als abstrakte Wissenschaft, sondern ähnlich einer Naturwissenschaft auffassen (vgl. Burscheid & Struve, 2020). Ein Impuls, der durch das Projekt DigiMath4Edu für Lehrkräfte gegeben wird, die bewusste didaktische Entscheidung in Konzeption und Durchführung zu treffen, mit empirischen Objekten als den mathematischen Objekten des Mathematikunterrichts zu arbeiten. Die empirischen Objekte (vgl. Abbildungen) dienen im Unterricht mit diesem didaktischen Prinzip nicht zur Veranschaulichung eigentlich abstrakter mathematischer Begriffe, sondern die Objekte sind die Gegenstände des Unterrichts. In Teilprojekt P4 werden mathematische Lehr-Lernprozesse mit digitalen Medien vor dem Theoriehintergrund eines empirisch-gegenständlichen Mathematikunterrichts untersucht.
Im Fokus stehen dabei die folgenden Ziele:
- Beschreibung und Analyse mathematischen (Schüler:innen-)Wissens in empirischen Kontexten mit digitalen Medien.
- Praxisnahe Aufbereitung des Konzeptes empirischer Theorien im Kontext digitaler Medien (Handreichung empirisch-orientierter Mathematikunterricht mit digitalen Medien).
Veröffentlichungen:
- Geplanter Beitrag in folgendem Sammelband: Dilling, F., Pielsticker, F., & Witzke, I. (2021). Mathematische Lehr-Lernprozesse im Kontext digitaler Medien Band 2.
- Geplanter Beitrag in MNU: Dilling, F., Pielsticker, F., Schneider, R., & Vogler, A. (2020). 3D-Druck in einem empirisch-gegenständlichen Mathematikunterricht.
- Dilling, F. (2021). Begründungsprozesse im Kontext von (digitalen) Medien im Mathematikunterricht. Wissensentwicklung auf der Grundlage empirischer Settings. Dissertation.
- Dilling, F. (2020, online first). Zur Rolle empirischer Settings in mathematischen Wissensentwicklungsprozessen – eine exemplarische Untersuchung der digitalen Funktionenlupe. Mathematica Didactica. Abrufbar unter: Link
- Dilling, F., & Pielsticker, F. (Hrsg). (2020). Mathematische Lehr-Lernprozesse im Kontext digitaler Medien. Empirische Zugänge und theoretische Perspektiven. Wiesbaden: Springer. Unter: Link
- Dilling, F., Pielsticker, F., & Witzke, I. (2020). Empirisch-gegenständlicher Mathematikunterricht im Kontext digitaler Medien und Werkzeuge. In F. Dilling, & F. Pielsticker (Hrsg.), Mathematische Lehr-Lernprozesse im Kontext digitaler Medien. Empirische Zugänge und theoretische Perspektiven (S. 1-27). Wiesbaden: Springer. Unter: Link
- Dilling, F., Pielsticker, F. & Witzke, I. (2019, online first). Grundvorstellungen Funktionalen Denkens handlungsorientiert ausschärfen – Eine Interviewstudie zum Umgang von Schülerinnen und Schülern mit haptischen Modellen von Funktionsgraphen. Mathematica Didactica. Abrufbar unter: Link
- Dilling, F. & Witzke, I. (2020). The Use of 3D-printing Technology in Calculus Education – Concept formation processes of the concept of derivative with printed graphs of functions. Digital Experiences in Mathematics Education, 6(3), 320-339. Abrufbar unter: Link
- Pielsticker, F. (2020). Mathematische Wissensentwicklungsprozesse von Schülerinnen und Schülern. Fallstudien zu empirisch-orientiertem Mathematikunterricht am Beispiel der 3D-Druck-Technologie. Wiesbaden: Springer Spektrum. Unter: Link
- Pielsticker F., Vogler, A., & Witzke, I. (2020). Argumentieren – Wissen sichern und erklären. In F. Dilling, & F. Pielsticker (Hrsg.), Mathematische Lehr-Lernprozesse im Kontext digitaler Medien. Empirische Zugänge und theoretische Perspektiven (S. 127-159). Wiesbaden: Springer. Unter: Link
- Pielsticker, F., & Witzke, I. (2020). Jede Menge Mathematik. Mathematiklehren und -lernen mit (CAD-)Programmen am Beispiel von Tinkercad™. In G. Pinkernell, & F. Schacht (Hrsg.), Digitale Kompetenzen und Curriculare Konsequenzen, Herbsttagung vom 27. bis 28. September 2019 an der Pädagogischen Hochschule Heidelberg des Arbeitskreises Mathematikunterricht und digitale Werkzeuge in der Gesellschaft für Didaktik der Mathematik. Hildesheim: Franzbecker.
Vorträge:
| 28.09.2019 | AK MDW Herbsttagung (Heidelberg) | Begriffsentwicklungsprozesse im Mathematikunterricht mit neuen Medien. Theoretische Perspektiven und empirische Einsichten am Beispiel der 3D-Druck-Technologie |
|
13.03.2019 |
4th Interdisciplinary Scientific Conference Mathematical Transgressions (ISCMT) (Cracow) | Concept Building in Mathematics Classrooms using New Media: Theoretical Perspectives and Empirical Insights on the Example of 3D-Printing Technology |
| 25.10.2018 | Adams State University (Colorado – Alamosa) | Concept Building in Mathematics Classrooms using New Media: Theoretical Perspectives and Empirical Insight on the Example of 3D-Printing Technology |
| 19.10.2018 | Florida State University (Tallahassee) | Concept Building in Mathematics Classrooms using New Media: Theoretical Perspectives and Empirical Insight on the Example of 3D-Printing Technology |
| 01.11.2019 | AK Mathematik und Bildung Herbsttagung (Siegen) | Zur Bedeutung empirischen Arbeitens im Kontext digitaler Medien und Werkzeuge |
| 29.09.2020 | GDM-Onlinetagung (Würzburg) | Wissensentwicklungsprozesse mit Darstellungen von empirischen Objekten - das CMC-Modell |