Gymnasium der Stadt Lennestadt
Schwerpunktthema: VR & AR –moderne Technik trägt zur Kompetenzerweiterung in der Geometrie bei
Unterrichtsassistentinnen: Visarius, Tatjana & Wollny, Isabell
Berichte der Unterrichtsassistentinnen
In den vergangenen Projektmonaten konnten wir wieder viele Unterrichtsvorhaben am Gymnasium der Stadt Lennestadt im Rahmen von DigiMath4Edu umsetzen. Diese sorgten für einen spannenden, erkenntnisreichen und abwechslungsreichen Mathematikunterricht mit digitalen Medien.
Stochastik praktisch erfahrbar machen - Erstellung und Testung von manipulierten Würfeln in der 8. Klasse
In der achten Klasse von Frau Borgard führten wir eine Unterrichtseinheit mit dem 3D-Drucker zum Themenbereich der Stochastik durch. In der Unterrichtseinheit sollten die Schülerinnen und Schüler in Kleingruppen einen Würfel erstellen, bei dem ein Vorteil in einem Gewinnspiel mit Würfeln erzielt werden kann. Zunächst wurde den Schülern und Schülerinnen das Gewinnspiel vorgestellt. Dann überlegten sie, welche Augenzahlen bei diesem Gewinnspiel förderlich und welche zu vermeiden sind und erstellten die Skizze eines Würfels, den sie für die Anforderungen des Gewinnspiels als besonders geeignet einschätzten. Die Ideen zur Manipulation waren zahlreich: Eine günstige Gewichtung des Würfels sollte beispielsweise über versteckte Bohrkörper im Inneren des Würfels oder verschieden tief ausgestanzte oder erhabene Zahlen auf den Würfelseiten erreicht werden. Außerdem gab es die Idee, die Auflageflächen der Würfelseiten durch eine Veränderung des Würfels in einen Quader oder auch herausragende Zahlen zu beeinflussen und so das Verhalten des Objekts beim Würfeln zu verändern.
In der nächsten Stunde wurden die Würfel mit dem CAD-Programm Tinkercad als 3D-Modell entworfen. Obwohl die Handhabung des Programms von einigen Schülern und Schülerinnen zunächst als anspruchsvoll wahrgenommen wurde, hatten alle Gruppen am Ende der Stunde ihren Würfel im Programm erstellt.
Die Würfel wurden danach mit den 3D-Druckern ausgedruckt und von den Schülern und Schülerinnen in der nächsten Stunde getestet: Jede Gruppe sollte mit ihrem Würfel hundert Mal würfeln und ihre Ereignisse zunächst in einer Strichliste festhalten und danach die absoluten und relativen Häufigkeiten der einzelnen Augenzahlen in eine selbst erstellte Tabelle eintragen. Im Anschluss präsentierten die einzelnen Gruppen ihren gezinkten Würfel mit der dahinterstehenden Konstruktions-Idee im Plenum sowie die Ergebnisse ihrer Testung, so wurden nicht nur inhaltliche Kompetenzen im Bereich Wahrscheinlichkeiten und Häufigkeiten, sondern auch prozessbezogenen Kompetenzen im Bereich Kommunizieren und Darstellen gefördert. Gemeinsam überlegten die Schülerinnen und Schüler, welche Würfel sich als besonders geeignet erwiesen haben und welche Würfel noch weiter verbessert werden könnten, um noch bessere Ergebnisse bei dem Gewinnspiel zu erzielen. Insgesamt wurden im Sinne des Lehrplans absolute und relative Häufigkeiten bestimmt, verglichen und gedeutet. Darüber hinaus diskutierten die Schülerinnen und Schüler, ob einhundert Würfelergebnisse ein ausreichender Datensatz für die Bestimmung der Güte der manipulierten Würfel darstellen. Somit wurde auch ein Bezug zum Gesetz der großen Zahlen hergestellt.

Die gezinkten Würfel
Zusammenhänge zwischen Funktionen und Ableitungen mit GeoGebra im Grundkurs untersuchen
In den Q1-Grundkursen bei Herrn Heim und Frau Michler waren die Eigenschaften ganzrationaler Funktionen Thema des Unterrichts. Der Lehrplan zur Sekundarstufe II im Fach Mathematik fordert als inhaltsbezogene Kompetenzen für die Qualifikationsphase, dass die Schüler und Schülerinnen notwendige Kriterien, Vorzeichenwechselkriterien sowie weitere hinreichende Kriterien zur Bestimmung von Extrem- und Wendepunkten verwenden. Außerdem sollen sie das Krümmungsverhalten des Graphen einer Funktion mithilfe der zweiten Ableitung beschreiben. Hinsichtlich der prozessbezogenen Kompetenzen sollen digitale Werkzeuge zum grafischen Darstellen von Funktionen und zur Berechnung der Ableitung einer Funktion an einer Stelle genutzt werden. Diese Forderungen des Lehrplans ließen sich mit der Nutzung von GeoGebra gut umsetzen.
Die Schülerinnen und Schüler nutzten GeoGebra zunächst, um Funktionen mit dem Grafikfenster einzuzeichnen und untersuchten dann in mehreren Unterrichtseinheiten in Sinne des entdeckenden Lernens die Zusammenhänge zwischen einer Funktion und ihren ersten drei Ableitungen mithilfe des Computer-Algebra-Systems. Sie leiteten somit das notwendige und hinreichende Kriterium für lokale Extrema und auch für Wendestellen selbst her. Dies regte außerdem zu Begründungsprozessen und zur Nutzung mathematischer Fachsprache an.
Zusätzlich lernten die Schüler und Schülerinnen in Vorbereitung auf das Abitur, in welchem das GymSL GeoGebra als CAS verwendet, wie sie die Software unterstützend nutzen können, um beispielsweise Extremwertprobleme zu lösen.
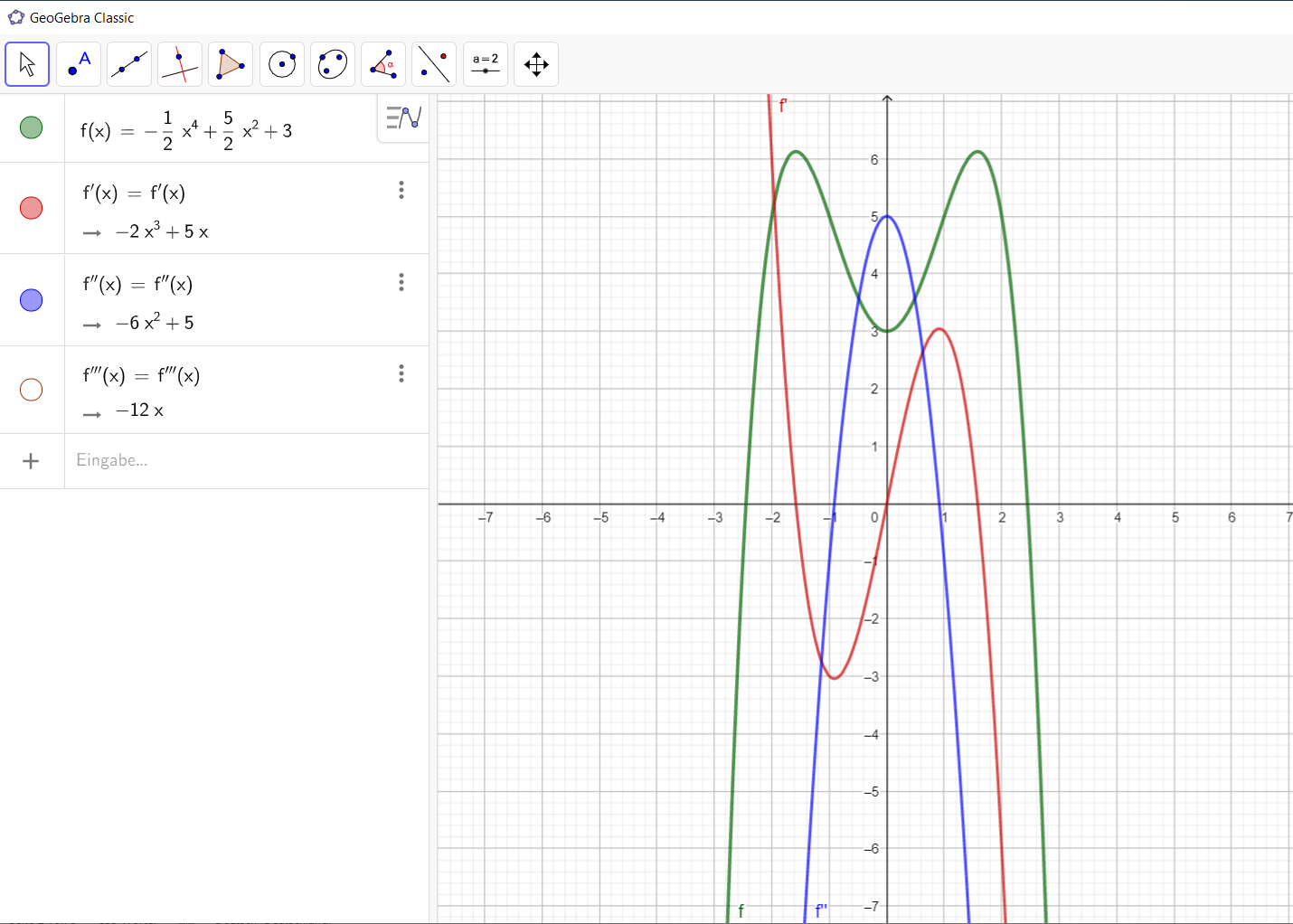 Hier wurden mit GeoGebra die ersten zwei Ableitungen einer Funktion f eingezeichnet und die dritte Ableitung berechnet.
Hier wurden mit GeoGebra die ersten zwei Ableitungen einer Funktion f eingezeichnet und die dritte Ableitung berechnet.3D-gedruckte Rotationskörper mithilfe von GeoGebra erstellen
Im Q2 Leistungskurs von Herrn Wagener wurden vor den Herbstferien Rotationskörper thematisiert. Zunächst erhielten die Schülerinnen und Schüler eine theoretische Einführung. Bei der Bearbeitung von Modellierungsaufgaben wurde den Lernenden deutlich, an welchen Stellen unseres alltäglichen Lebens Rotationskörper eine Rolle spielen. Sie sollten ein Sektglas ihrer Wahl gestalten, welches folgende drei Bedingungen erfüllen sollte:
- Das Sektglas muss 100ml fassen und eine Höhe von maximal 15cm haben.
- Das Sektglas muss dicht sein.
- Das Sektglas muss auf einer ebenen Fläche stehen können.
Am Ende dieser Einheit haben die Schülerinnen und Schüler ihr gedrucktes Sektglas vorgestellt und ihren Konstruktionsweg erläutert.
Mit Hilfe der 3D-Druck-Technologie konnten die Modellierungsideen der Schülerinnen und Schülern greifbar und somit empirisch überprüfbar werden. Gemeinsam überlegten und diskutierten sie an ihren Modellen, ob ihre Ideen umsetzbar sind und inwiefern sie ihre Modellierungen noch verbessern können. Mithilfe des 3D-Druckers werden aus Ideen und mentalen Vorstellungen reale Produkte, die kritisch beurteilt werden können und zur Reflexion anregen.
Auf Seiten der Lernenden gab es nachfolgende positive Rückmeldungen: „Jetzt weiß ich wofür ich das (Rotationskörper) brauche!“ und „Das ist richtig toll, wenn man sein eigenes, designtes Produkt in den Händen halten kann und sagen kann DAS IST VON MIR. Da ist man schon stolz!“. Auch Herr Wagener stellte mit Begeisterung fest, dass die Lernenden eigenständig anfingen ihre neu erworbenen mathematischen Kenntnisse zu Rotationskörpern mit mathematischen Kenntnissen aus vergangenen Schuljahren verknüpften und somit ein tiefgehendes Verständnis von der Mathematik aufbauen konnten. „Es ist schön zu sehen, mit wieviel Spaß sich die Schülerinnen und Schüler mit den mathematischen Inhalten auseinandersetzen und ihre eigenen Ideen einbringen. Die Stunde läuft einfach von selbst!“ (Herr Wagener). Das Thema „Rotationskörper“ ist ein komplexer Inhalt, welcher für viele Schülerinnen und Schüler auf rein visueller Ebene schwer begreifbar ist. Durch die Verbindung von GeoGebra und dem 3D-Druck wird eine neue Art von Anschauung gewährleistet, die das Interesse der Lernenden weckt und zu einem tiefergreifenden mathematischen Verständnis des Inhalts beitragen kann.
 |  |  |  |  |
 | ||||
Anschauungsobjekte für das Rechnen mit Brüchen 3D-drucken
In der Klasse 6c wurde das Thema der Bruchrechnung eingeführt. Anfangs haben die Lernenden oft Schwierigkeiten Brüche in gleichnamige Brüche umzuwandeln. Diese Thematik ist bis zum Abitur von Relevanz und sollte daher bereits im Einstieg von den Schülerinnen und Schülern verstanden werden. Anhand von 3D-gedruckten Bruchstücken (vgl. Foto) lernten die Schülerinnen und Schüler durch das Legen und Vergleichen dieser Stücke, dass beispielsweise 1/2 und 2/4 denselben Anteil eines Ganzen darstellen. Hierauf aufbauend konnten die Schülerinnen und Schüler einfach Additions- und Subtraktionsaufgaben mit Bruchzahlen lösen. Kommentare wie „Das ist ja cool, so sieht man wieviel was ist!“ oder „Das ist doch gar nicht schwer. Das macht doch Spaß!“ überwogen in der Unterrichtsstunde. Auch die Lehrerin war begeistert, wie schnell die Lernenden den Sachverhalt verstanden hatten: „Das ist echt super. Brüche sind immer ein schwieriges Thema, wo viele nicht mehr mitkommen. Aber hier sind alle sehr motiviert und begreifen den mathematischen Sachverhalt recht schnell“. Mithilfe des 3D-Druckers kann an die Lerngruppe angepasstes Anschauungsmaterial gedruckt werden. Die Bruchstücke könnten von den Schülerinnen und Schülern auch selbst konstruiert werden, was wiederum die Modellierungskompetenzen fördern würde.

GeoGebra und VR
Klasse 7 - Dreiecke konstruieren mithilfe von GeoGebra
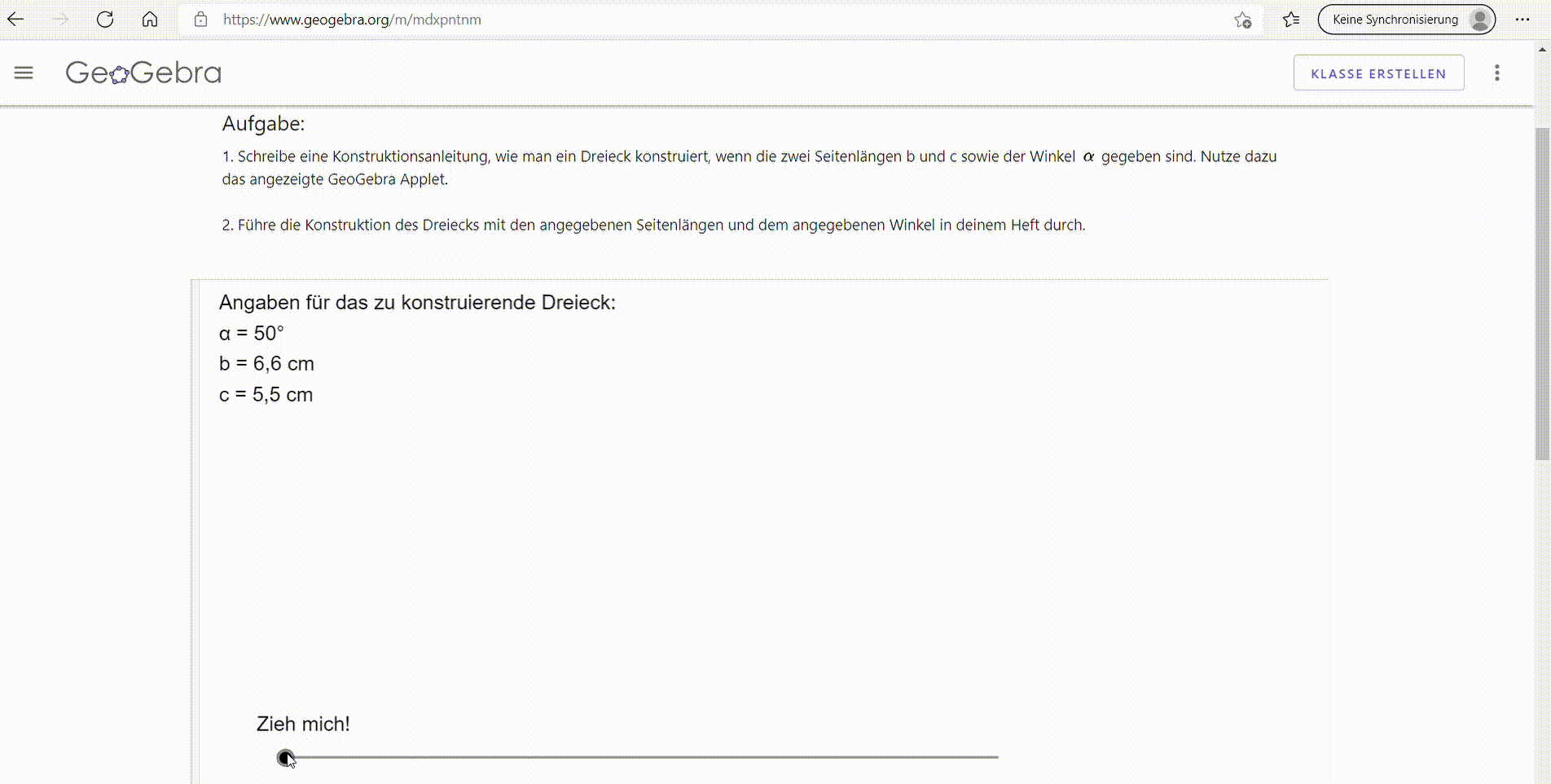
Der Geometrieunterricht der siebten Klasse musste in diesem Frühjahr weitgehend im Digitalunterricht durchgeführt werden. Um die Konstruktion von Dreiecken zu veranschaulichen, wurde mit GeoGebra Classroom gearbeitet: Die Schüler*innen bearbeiteten Applets, die ihnen die Konstruktion von Dreiecken nach verschiedenen Kongruenzsätzen schrittweise anzeigten. Dazu sollten die Schüler*innen eine Konstruktionsanleitung verfassen. Anschließend wurden Konstruktionen von Dreiecken analog und digital mit GeoGebra durchgeführt. Die Lehrkräfte konnten über GeoGebra Books die Arbeitsergebnisse der Schüler*innen überprüfen und über in die Aufgaben integrierte Fragen einsehen, wie der Schwierigkeitsgrad bei den Lernenden eingeschätzt wurde.
Schülerin der siebten Klasse: „Das Lernen mit GeoGebra Classroom hat mir Spaß gemacht und hat auch gut funktioniert. Ich habe auch viel gelernt. Das können wir gerne nochmal machen.“
Im Präsenzunterricht wurde eine Dokumentenkamera genutzt, da einige Schüler*innen durch den Digitalunterricht bedingt noch Probleme mit den geometrischen Werkzeugen Zirkel und Geodreieck hatten. Stärkere Schüler*innen konnten über die Dokumentenkameras die richtige Handhabung dieser Werkzeuge dem Rest der Klasse noch einmal demonstrieren.
Q1 LK - Analytische Geometrie entdecken mit GeoGebra und Virtual Reality
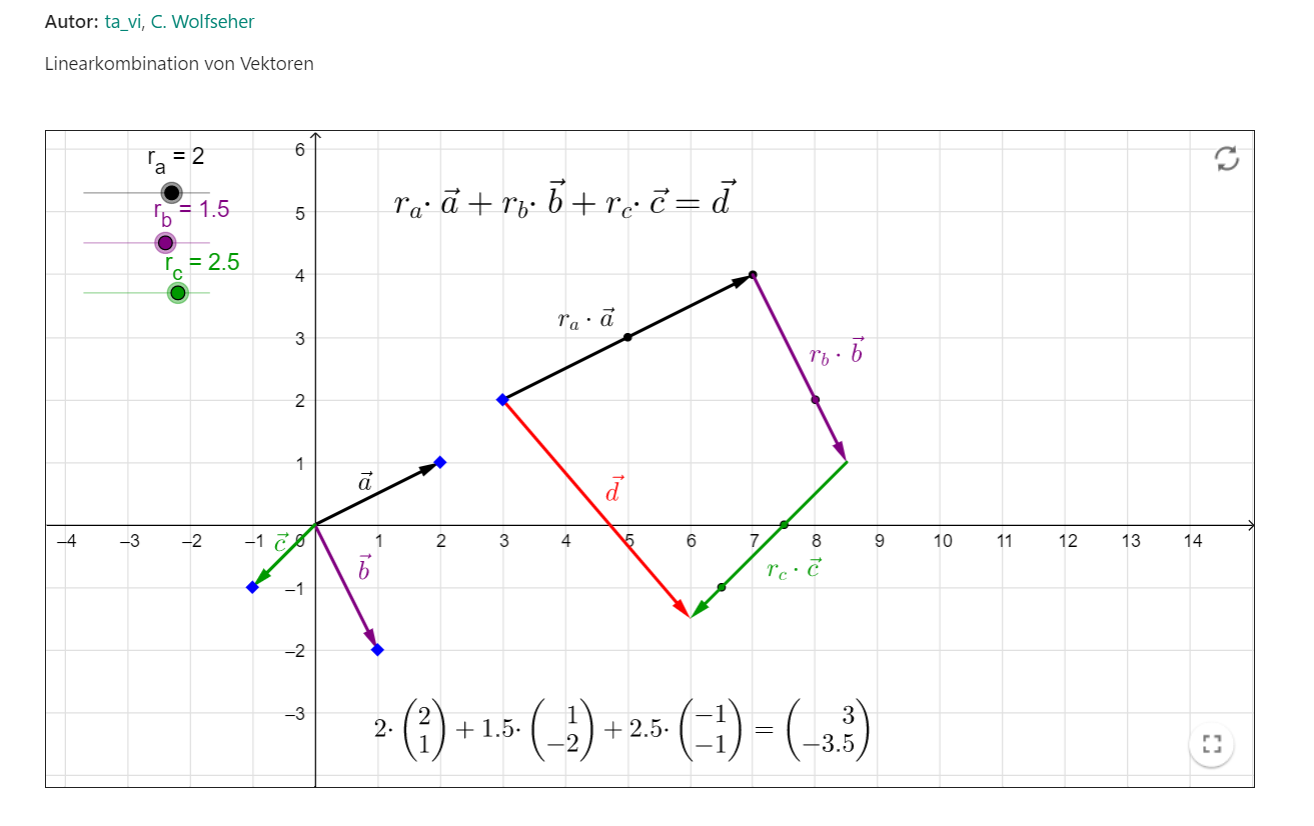
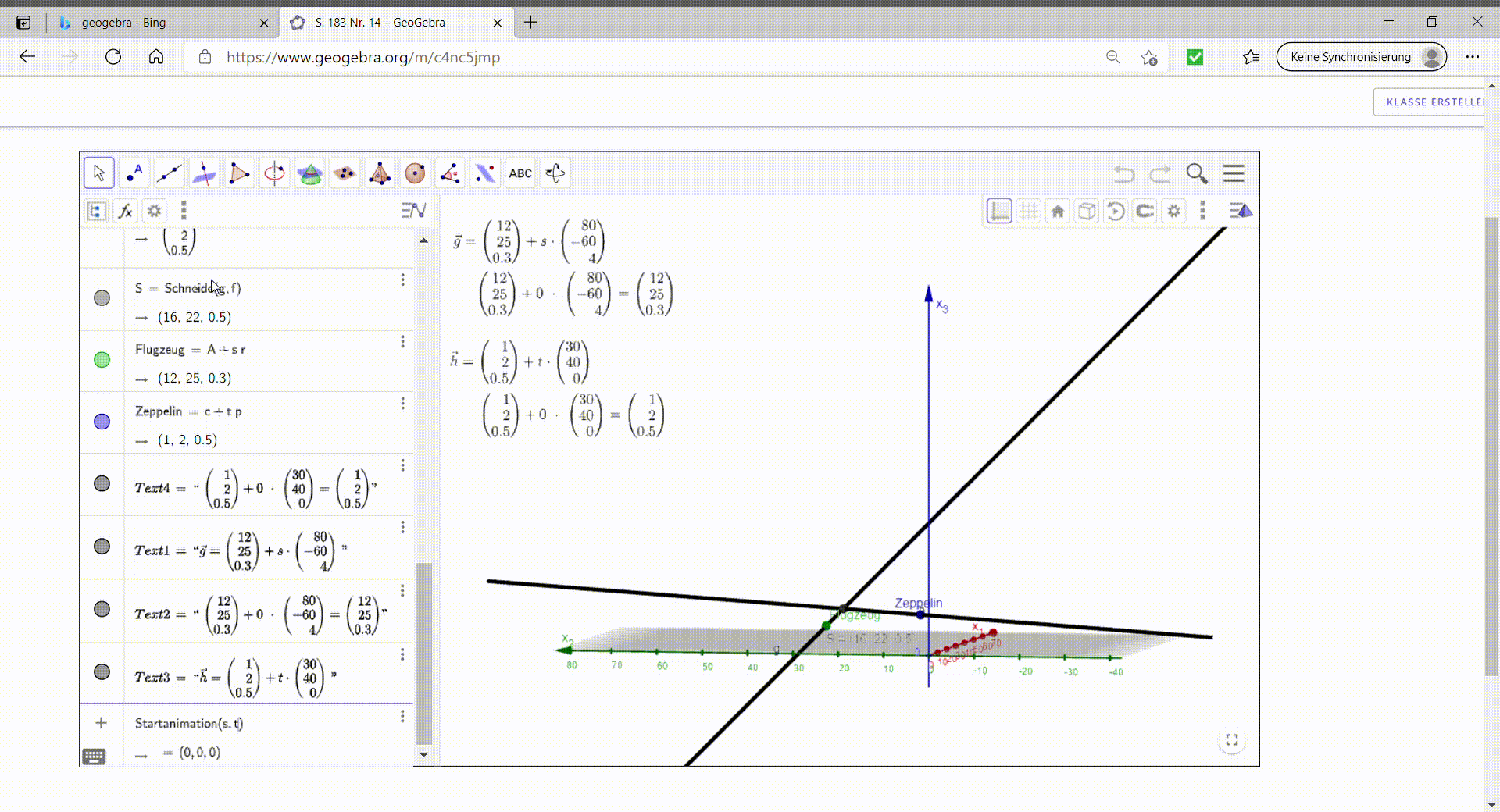
In dem Q1 Leistungskurs von Herrn Soemer wurden zahlreiche GeoGebra Applets genutzt, um den Schüler*innen die Sachverhalte der analytischen Geometrie (Linearkombinationen von Vektoren, Lagebeziehungen von Geraden, Ebenen in Parameterform, Abstandsformeln etc.) zu veranschaulichen. Dies war besonders für die schwächeren Lernenden hilfreich. Zusätzlich wurden Lernprozesse spannender gestaltet, indem die Schüler*innen mit Applets Sachverhalte wie den Zusammenhang von Skalarprodukt und Orthogonalität von Vektoren selbst entdecken konnten. Auch für gezieltes Abiturtraining konnte GeoGebra genutzt werden: Eine Abituraufgabe zur analytischen Geometrie wurde visualisiert und erklärt, wie der Einsatz von GeoGebra-Befehlen (welche auch im Abitur verwendet werden dürfen) das Lösen der Aufgaben erleichtern kann.
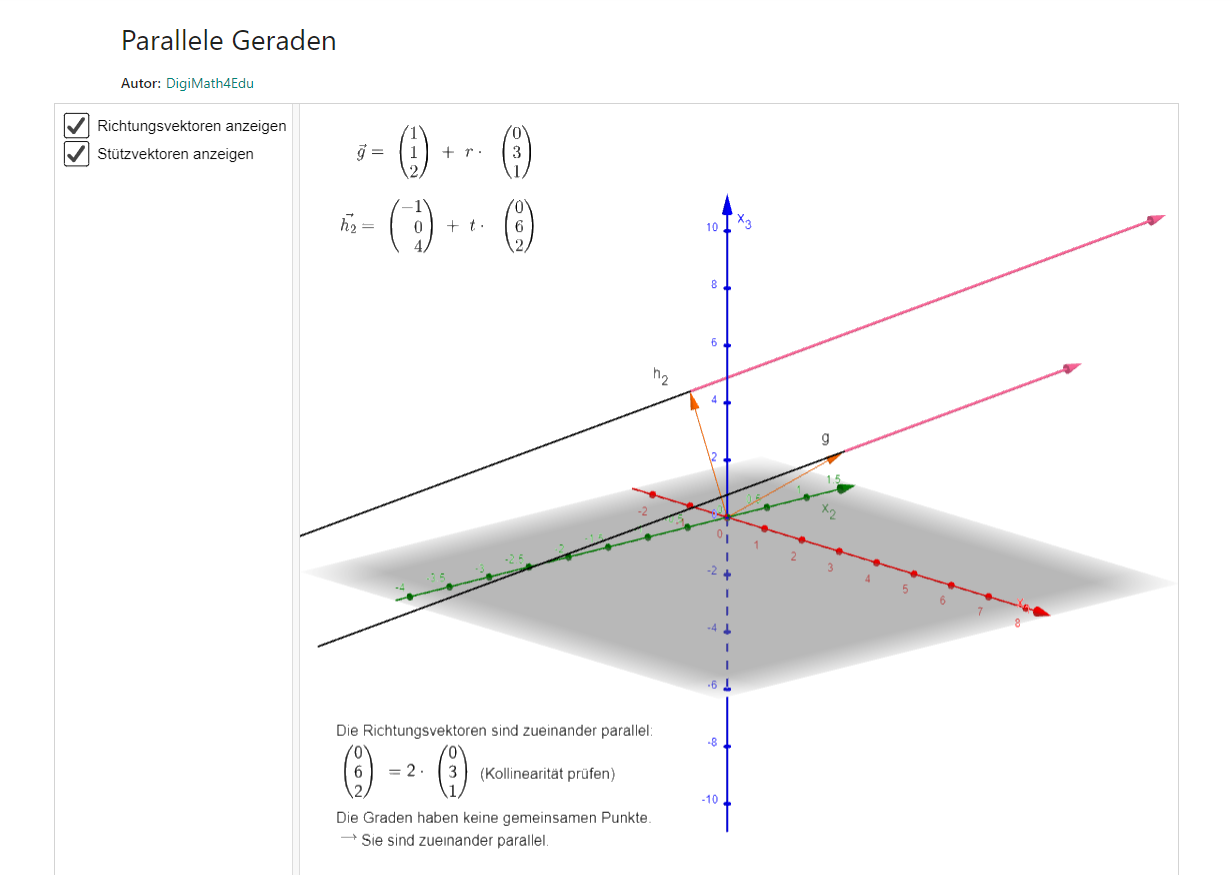 | 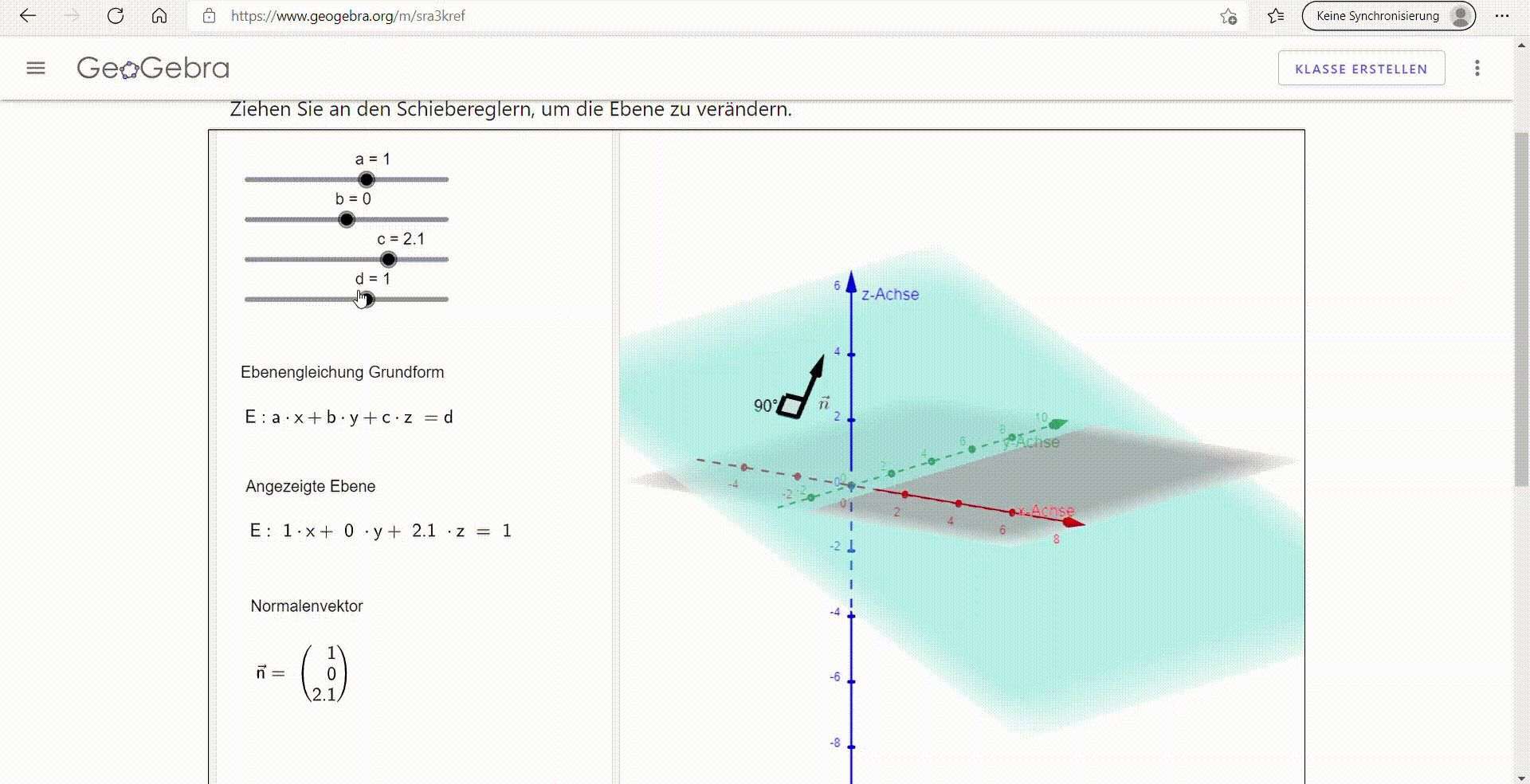 |
Im LK von Herrn Wagener wurden zudem Virtual Reality Brillen genutzt, um Ebenen in Koordinatenform zu veranschaulichen. In Partnerarbeit mussten sich die Schüler*innen mithilfe einer Anleitung die Funktionsweise der VR-Brille Oculus Quest erarbeiten und ihrem Partner die Lage von in Koordinatenform eingezeichneten Ebenen erklären. Die Universität Siegen konnte in dieser Unterrichtsstunde Erkenntnisse für ihr Forschungsinteresse zur Nutzung von Virtual Reality im Mathematikunterricht sammeln.
Schüler der des LK: „Zuerst dachte ich, dass GeoGebra reicht, weil man damit auch Ebenen zeichnen kann. Es war aber nochmal etwas anderes, die Ebenen im Raum zu sehen. Es hat Spaß gemacht, sich das Thema mit den VR-Brillen zu erarbeiten.“

Von Wimmelbildern und TinkerCAD
In der 5. Klasse ist, wie bereits im ersten Projektbericht erwähnt, die Anton-App sehr beliebt und es wurde mit dieser viel gearbeitet. Auch die Learningapps und GeoGebra fanden in der 5. Klasse ihren Einsatz im Bereich des Koordinantensystems und kamen positiv bei den Schülerinnen und Schülern an. Ein Wimmelbild zu den Themen Koordinantensystem und Flächeneinheiten diente als Klausurvorbereitung und versetzte die Schülerinnen und Schüler in eigenständiges Arbeiten. „Das ist cool!“ oder „Mal was anderes als Aufgaben aus dem Buch.“ waren Äußerungen, die diese Arbeitsphase prägten. Auch die Lehrkraft begeisterte sich für diese andere Art von Aufgabenbearbeitung und empfand es als eine gelungene Methode vor allem für die Vorbereitung auf die Klassenarbeit.

 |  |
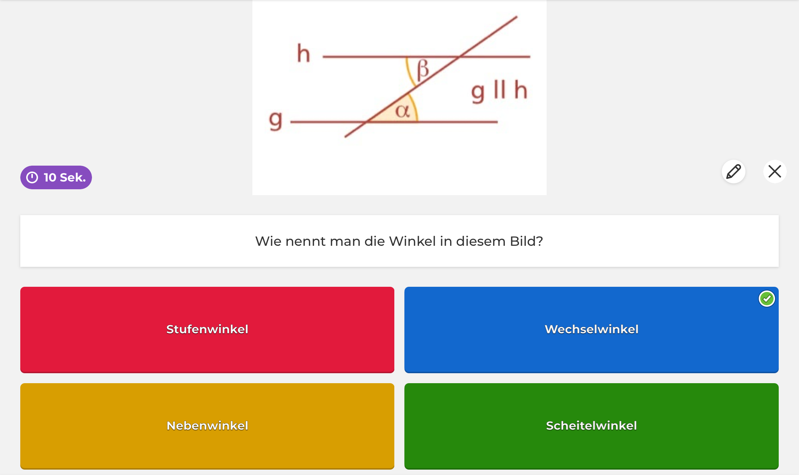 | 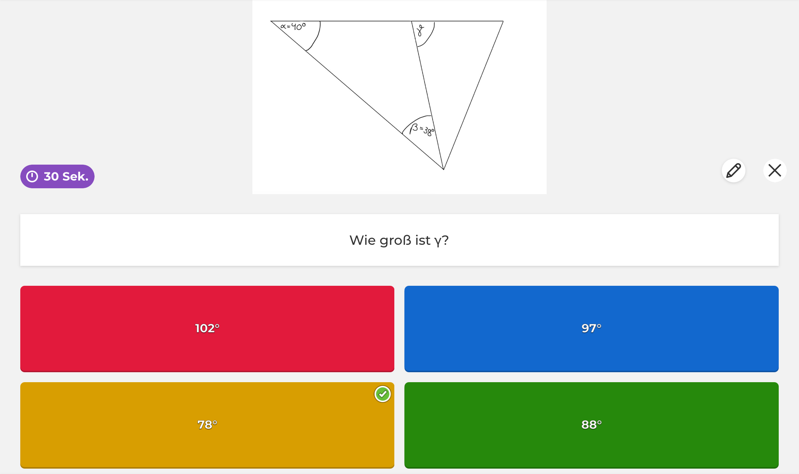 |
Ein weiteres Projekt in der 7. Klasse war ein Wimmelbild zu Prozentrechnung und Gleichungen als eine Wiederholung des Schuljahres. Diese zwei Themen wurden von den Schülerinnen und Schülern schwer aufgefasst und es gab viele Probleme in den Thematiken, weshalb zum Abschluss des Schuljahres zwei Unterrichtsstunden darauf verwendet wurden, um die Sachverhalte nochmal kompakt hervorzurufen. Für die Lernenden war es eine Abwechslung zu den Schulbuchaufgaben und auch die Lehrkraft empfand dies als eine gelungene Abwechslung. „Eine tolle Möglichkeit, dass die Schüler selbstständig die Sachverhalte nochmal mit Übungsaufgaben und Merkregeln durcharbeiten. Super! Das hat richtig gut geklappt.“ ist eine Aussage der Lehrkraft, welche im Nachhinein auch noch berichtet hat, dass die Lernenden die Themen ein Stück weit besser verstanden haben und es als einen guten Abschluss des Schuljahres empfunden haben. Die Schülerinnen und Schüler lernen neben den fachlichen Inhalten auch das selbstständige arbeiten und kontrollieren. Sie können sich aussuchen mit welchen Aufgaben sie beginnen und nach Bearbeitung dieser können sie auch eigenständig ihre Lösung mit der Musterlösung, welche hinterlegt ist, kontrollieren.
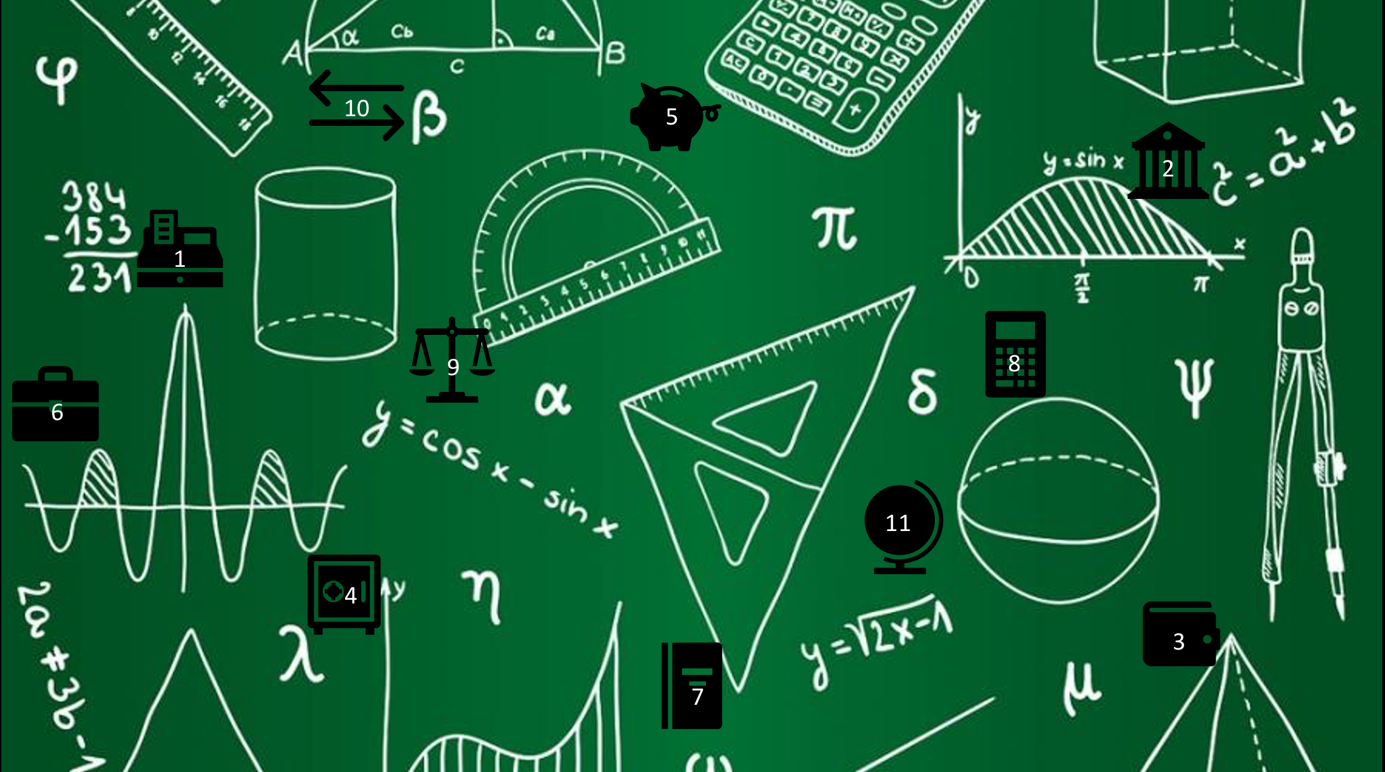
In dem Q1 LK kamen erstmals die VR-Brillen zum Einsatz zum Thema Ebenen in Koordinatenform. Die Schülerinnen und Schüler sollten sich zunächst mit dem digitalen Medium vertraut machen, dafür haben sie eine detaillierte Anleitung erhalten, wie sie die VR-Brillen zu nutzen haben und welche Funktionen für was gut sind. Anschließend sollten sie Ebenen, die in Koordinatenform angegeben waren in der VR-Brillen-App zeichnen lassen und die Ebenen auf ihre besondere Lage untersuchen und gegebenenfalls Merkmale der Besonderheiten nennen. Manche Lernenden waren skeptisch, ob es nicht dasselbe ist wie GeoGebra von der Anschauung her, aber diese Schülerinnen und Schüler konnten recht schnell vom Gegenteil überzeugt werden „Wow, das habe ich nicht erwarten. Das ist ja ganz anders. Man kann ja sogar in die Ebene rein.“ Vor allem die Visualisierung war für die meistens ein positiver Effekt, der sich auf das räumliche Verständnis dieser ausgewirkt hat „Eigentlich kann ich mir sowas gar nicht richtig vorstellen. Schon gar nicht im Kopf. Bei GeoGebra geht es, aber ich hier ist das nochmal was ganz anderes. Man ist richtig in diesem Raum drin und blendet alles andere aus.“. Die Anwendung der VR-Brillen wurde gemeinsam mit den Schülerinnen und Schüler besprochen und diskutiert was die Nachhaltigkeit angeht und die Benutzung im Unterricht. Hier waren sich alle einig, dass dieses digitale Medium Potential hat und besonders in der analytischen Geometrie noch von Bedeutung sein wird. Um zu schauen, ob die Lernenden wirklich etwas mitgenommen haben aus dem Unterricht mit den VR-Brillen wurde ein paar Stunden später nochmal eine VR-Brillen-Stunde durchgeführt, wo die Lernenden jedoch einen Transfer leisten mussten. Sie mussten ihr erworbenes Wissen über die besondere Lage der Ebenen anwenden, um die Koordinatenform herauszufinden. Als visuelle Unterstützung sollen sie daher die Ebenen in der VR-Brillen-App wieder zeichnen lassen und auf ihre Merkmale hin analysieren. Dies hat äußerst gut geklappt, woran man auch sehen kann, dass die VR-Brillen nicht nur eine Spielerei sind, sondern auch nützlich sein können und man auch im Mathematikunterricht von ihnen profitieren kann.
Ein ganz großes digitales Medium, welches in fast jeder Unterrichtstunde im Q1 LK Einsatz findet, ist GeoGebra. Sei es GeoGebra Classic, GeoGebra 3D oder der Grafikrechner, sie sind mittlerweile unverzichtbar geworden. Dies ist nicht wunderlich, da die Lernenden GeoGebra mit allen Funktionsweise in ihrem Abi nutzen dürfen und daher der Umgang mit diesem intensiv geübt werden muss. Insgesamt empfinden die Schülerinnen und Schüler die Applets in GeoGebra sehr gut für ein tiefergehende Verständnis. Besonders die Dreidimensionaltiät, die GeoGebra bietet, erleichtert vielen Lernenden die mathematische Perspektive der Sachverhalten zu verstehen. Hier nun exemplarisch einige Kommentare zu den verschiedenen Themen, die die Effekte des digitalen Mediums im Unterricht darstellen:
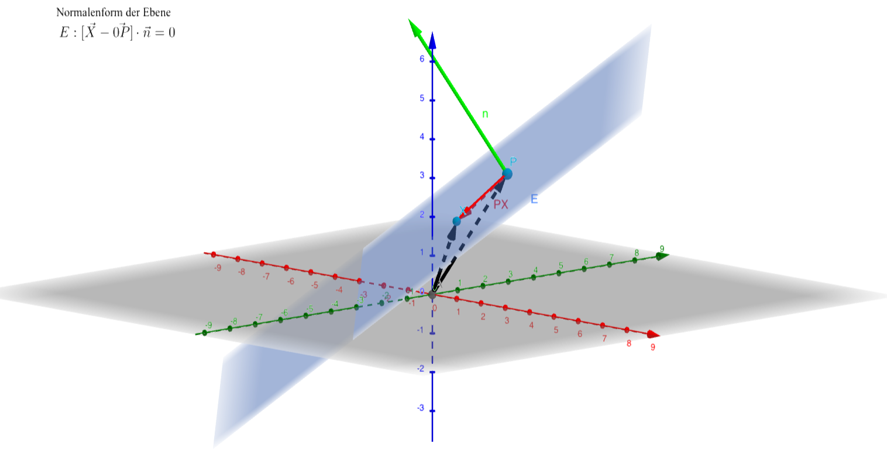
- Koordinatenebenen und -achsen
-> „Schönes Applet, um auch Ebenen zu zeichnen.“, „Der Durchstoßpunkt ist wunderbar zu sehen.“ (Lehrer)
-> „Toll wie der Punkt mitgeht je nachdem wie man die Ebene verändert.“ (Schüler)
-> „Geht ganz schnell.“, „Die Visualisierung führt zu einem besseren Verständnis.“ (Schülerin) - Geradengleichung (in Parameterform)
-> „Ziemlich angebracht, besser als das Vorstellen aus dem Kopf heraus.“ (Schüler)
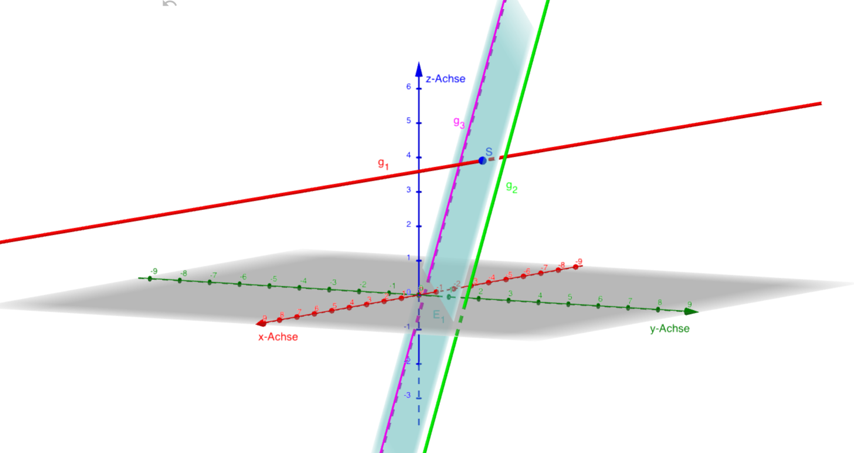
-> „Verschiedene Ansichten, Anschauung schaffen.“ (Lehrer) - gegenseitige Lage von Geraden
-> „Prima, sehr anschaulich!“ (Schülerin)
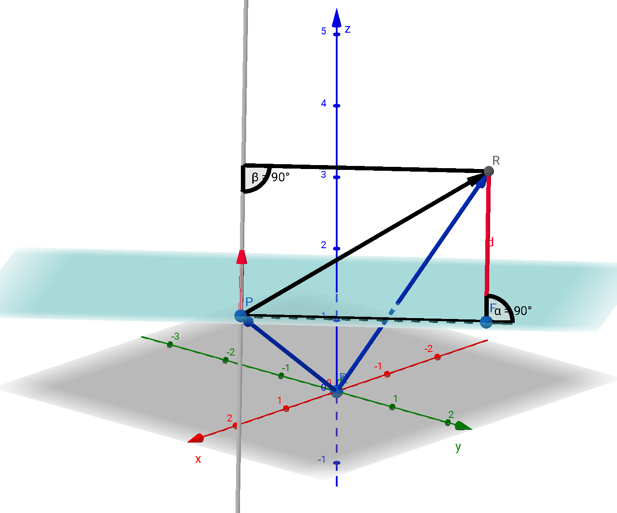
-> „Endlich hat man eine richtige Ansicht. Sonst rechnet man alles aus, aber man kann sich nichts darunter vorstellen. Jetzt ist das anders.“ (Schüler) - Darstellung des Normalenvektor aus dem Vektorprodukt
-> „Prima. Tolle Darstellung.“ (Lehrer)
-> „Sehr gut, dass der rechte Winkel zu erkennen ist.“ (Schüler)
Es wurden aber auch andere Inhalte thematisiert, wie beispielsweise Ebenen in Parameter- und Koordiantenform, die Hesse’sche Normalform, der Abstand windschiefer Geraden oder die Schnittwinkel zwischen zwei Geraden, zwei Ebenen und einer Geraden und einer Ebene.
 |  |
 |  |
GeoGebra-Anwendungen in verschiedenen Jahrgangsstufen
Trotz Digitalunterrichts konnte das Projekt DigiMath4Edu dank der tollen Zusammenarbeit mit den Lehrkräften des GymSL in Lennestadt von Anfang an mit vielen guten Technologie-Einsätzen im Unterricht starten. Ich wurde für die ersten zwei Monate dem Unterricht von Frau Gerbe, einer schulinternen Projektbetreuerin von DigiMath4Edu, zugeteilt und wurde in den von ihr unterrichteten Klassen sieben, neun und zehn als Unterrichtsassistentin für digitale Medien tätig.
Da das GymSL als technisch versierte MINT-EC-Schule durch die Einrichtung der Microsoft Dienste Teams und OneNote für alle Schüler*innen bereits die technischen Voraussetzungen für einen gelungenen Digitalunterricht geschaffen hatte, konnte ich mich mit den Lehrkräften von Anfang an darauf fokussieren, wie wir mithilfe didaktisch überlegter Medieneinsätze das Mathematikverständnis der Schüler*innen verbessern konnten.
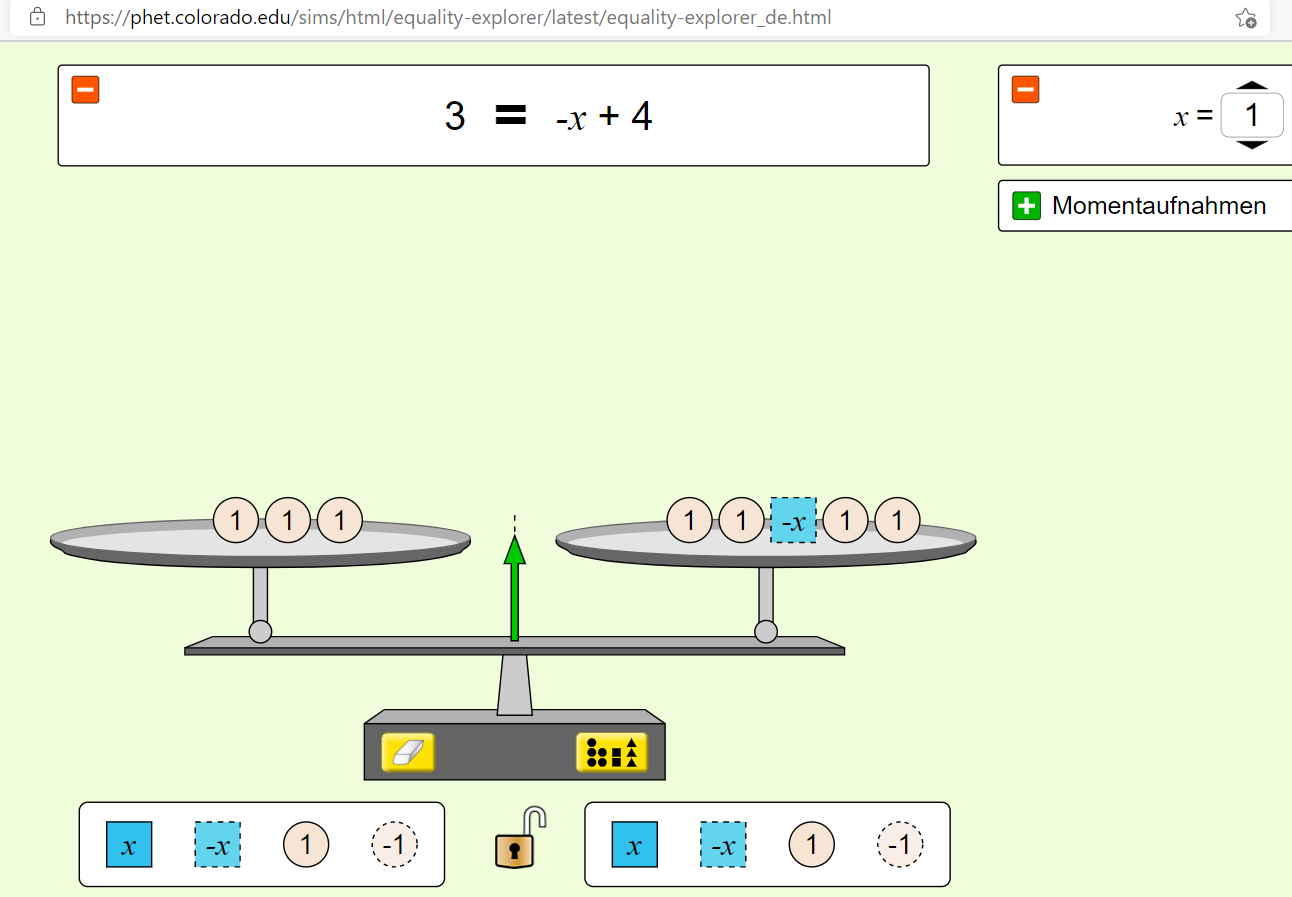
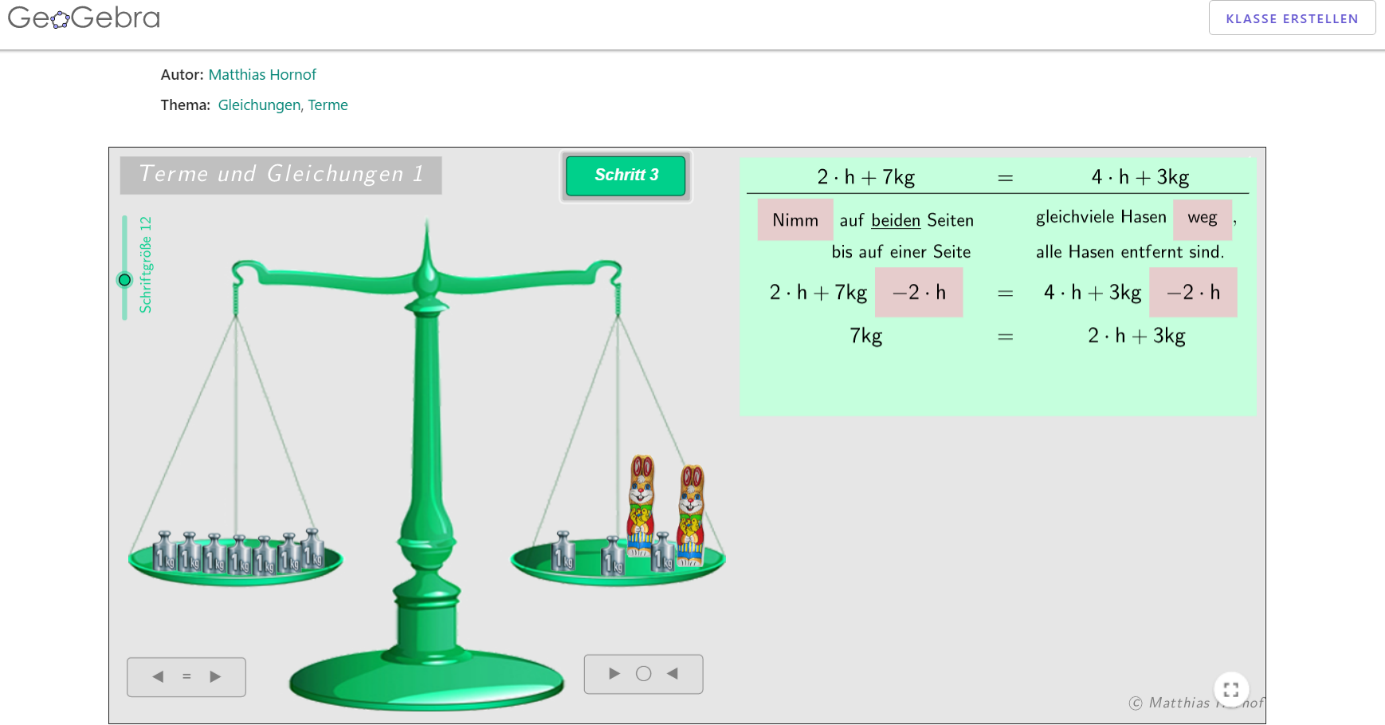
In der siebten Klasse stand das Lösen von Gleichungen mittels Äquivalenzumformungen auf dem Lehrplan. Im alltäglichen Schulunterricht wird das Lösen von Gleichungen oft an einem Modell einer Waage veranschaulicht, bei dem jeder Gleichungsseite einer Waagschale zugeordnet wird und bei Vereinfachungsschritten auf beiden Seiten dieselben Operationen getätigt werden müssen, um das Gleichgewicht der Waagschalen zu erhalten. Im Distanzunterricht war eine solche Veranschaulichung anhand einer analogen Waage jedoch schwierig und eine Lösung musste gefunden werden. Nach einiger Recherche stand jedoch fest, dass auch das Internet geeignete Visualisierungen des sogenannten Waagenmodells bietet und teilweise sogar mehr Möglichkeiten bereitstellt als die Arbeit mit einer analogen Waage. Mithilfe verschiedener Internetseiten und einem GeoGebra-Applet wurde spielerisch ein Zusammenhang von Waagschalenoperationen und Gleichungen hergestellt und visualisiert, was seitens der Lernenden beliebt war und das Verständnis gefördert hat.
|
|
In der zehnten Klasse wurde der Zusammenhang von Sekanten, Tangenten, Differenzenquotient und Ableitungen durch GeoGebra visualisiert. Dazu habe ich eine Anwendung konzipiert, bei der der Abstand der beiden Schnittpunkte der Sekante mit einem Funktionsgraphen an einer beliebigen Stelle des Funktionsgraphen angenähert werden kann. Mithilfe einer detaillierten Anleitung konnten die Schüler*innen diese Datei selbst in GeoGebra konzipieren und somit zusätzlich ihre Fähigkeiten bei GeoGebra vertiefen: Diese Herausforderung wurde von den Schülern und Schülerinnen der EF gerne angenommen!
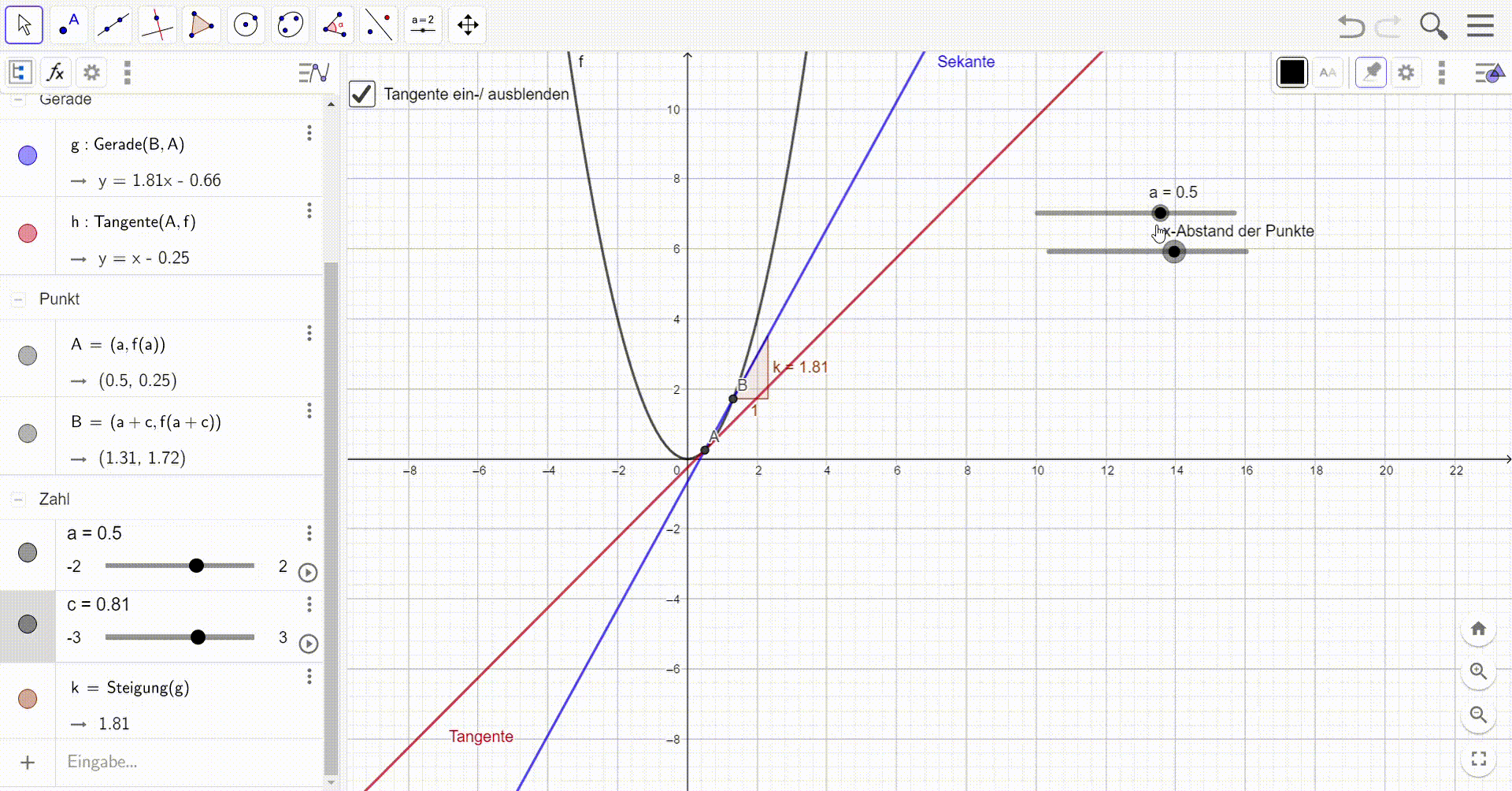
Diese GeoGebra Veranschaulichung programmierten die Schüler*innen mithilfe einer Anleitung auf dem eignen Gerät.
 Herr Heim, der das Script auch für seine EF genutzt hat, berichtet über das Feedback der Schüler*innen zu diesem digitalen Einsatz in der nachfolgenden Unterrichtsstunde:
Herr Heim, der das Script auch für seine EF genutzt hat, berichtet über das Feedback der Schüler*innen zu diesem digitalen Einsatz in der nachfolgenden Unterrichtsstunde:
Das Script ist fantastisch […]. Heute habe ich dann im Einstieg daran erinnert, dass die Stunde zwei Ziele hatte:
besseres Verständnis der o.g. Zusammenhänge erzeugen
sichereren Umgang mit GeoGebra ermöglichen
und jeder Schüler musste in der Begrüßungsrunde dazu Stellung nehmen, inwiefern die beiden Ziele erreicht wurden. Alle Schüler haben sich differenziert und positiv dazu geäußert! Sie fanden es interessant, sinnvoll und gaben an, die Zusammenhänge nun besser verstanden zu haben. Danach habe ich sie darauf hingewiesen, dass das Projekt auch ein Forschungsprojekt ist und wir froh über Verbesserungsvorschläge wären, zum Beispiel bei Stellen im Skript, bei denen sie Probleme hatten - gab es nicht!“
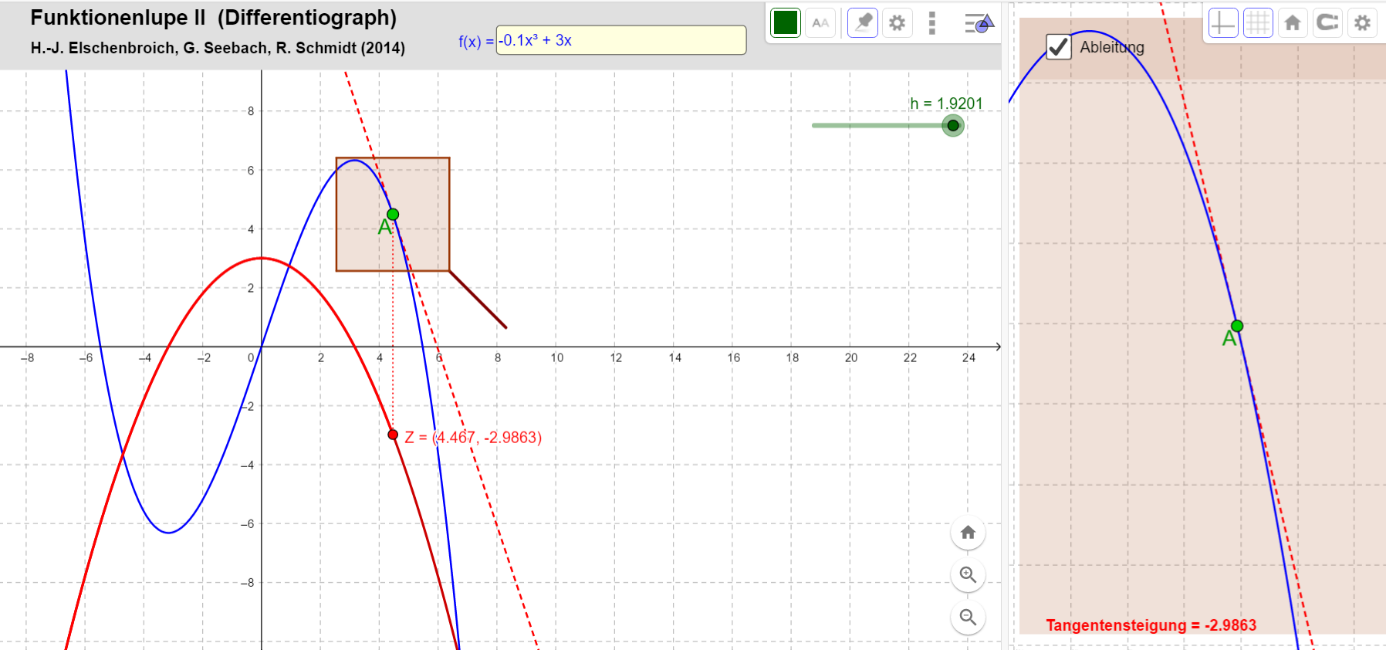
Der Zusammenhang zwischen der Tangentensteigung und der Ableitung wurde anhand der Funktionenlupe vertieft.
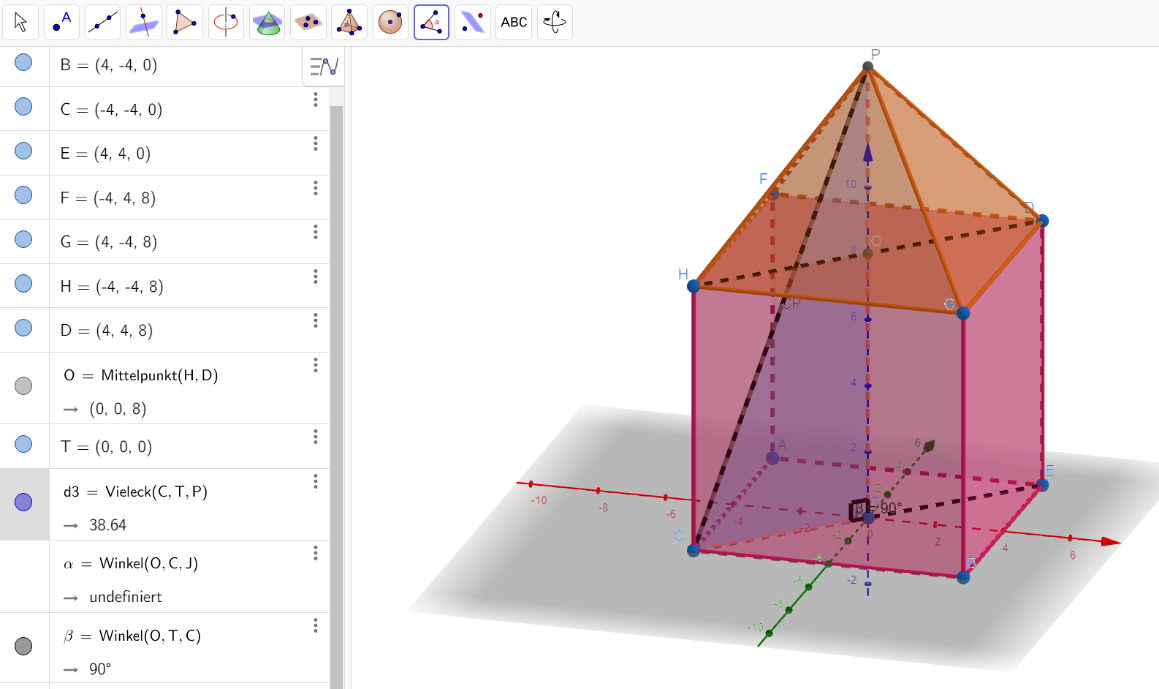
In der neunten Klasse fand bei der Beschäftigung mit Pythagoras in Körpern unter anderem GeoGebra 3D Verwendung, um Winkel und Strecken in Körpern anschaulicher zu machen. Im Anschluss wurden die Volumenformeln für Körper eingeführt und in diesem Zusammenhang die Volumenformel der quadratischen Pyramide anhand eines GeoGebra-Applets hergeleitet, um Mathematik als beweisende Disziplin erfahrbar zu machen.
|
|
Ab März wurde uns Unterrichtsassistentinnen erfreulicherweise ermöglicht, auch in den Präsenzunterricht einzusteigen: Isabell Wollny und ich betreuen nun auch die beiden Mathematik Leistungskurse der Q1 des GymSL.
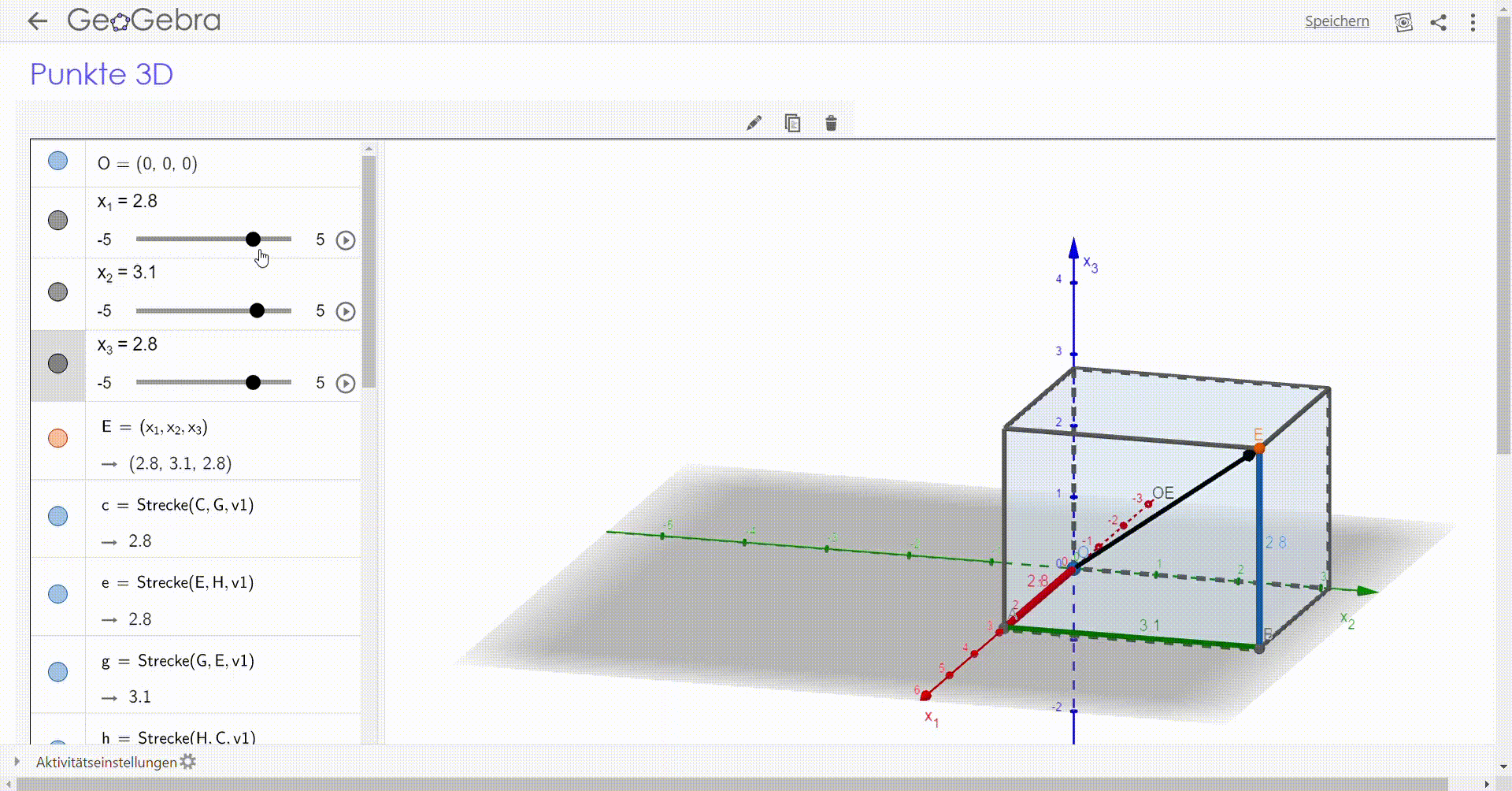
Dort unterstützen wir Herrn Soemer und Herrn Wagener momentan bei der Verwendung von digitalen Medien bei der Vermittlung von analytischer Geometrie. Herr Soemer und ich haben eine vielfältige Nutzung von GeoGebra 3D und GeoGebra Classic für diese Unterrichtseinheit vorgesehen. Punkte und Vektoren im Raum, Linearkombinationen von Vektoren sowie das Thema Geradengleichungen und Textaufgaben zu Geradenschnittpunkten wurden bereits erfolgreich anhand GeoGebra visualisiert und halfen den Schüler*innen, die geometrischen Vorgänge besser zu verstehen.
Selbst erstelltes Applet zur Visualisierung von Punkten und Vektoren im Raum. | |
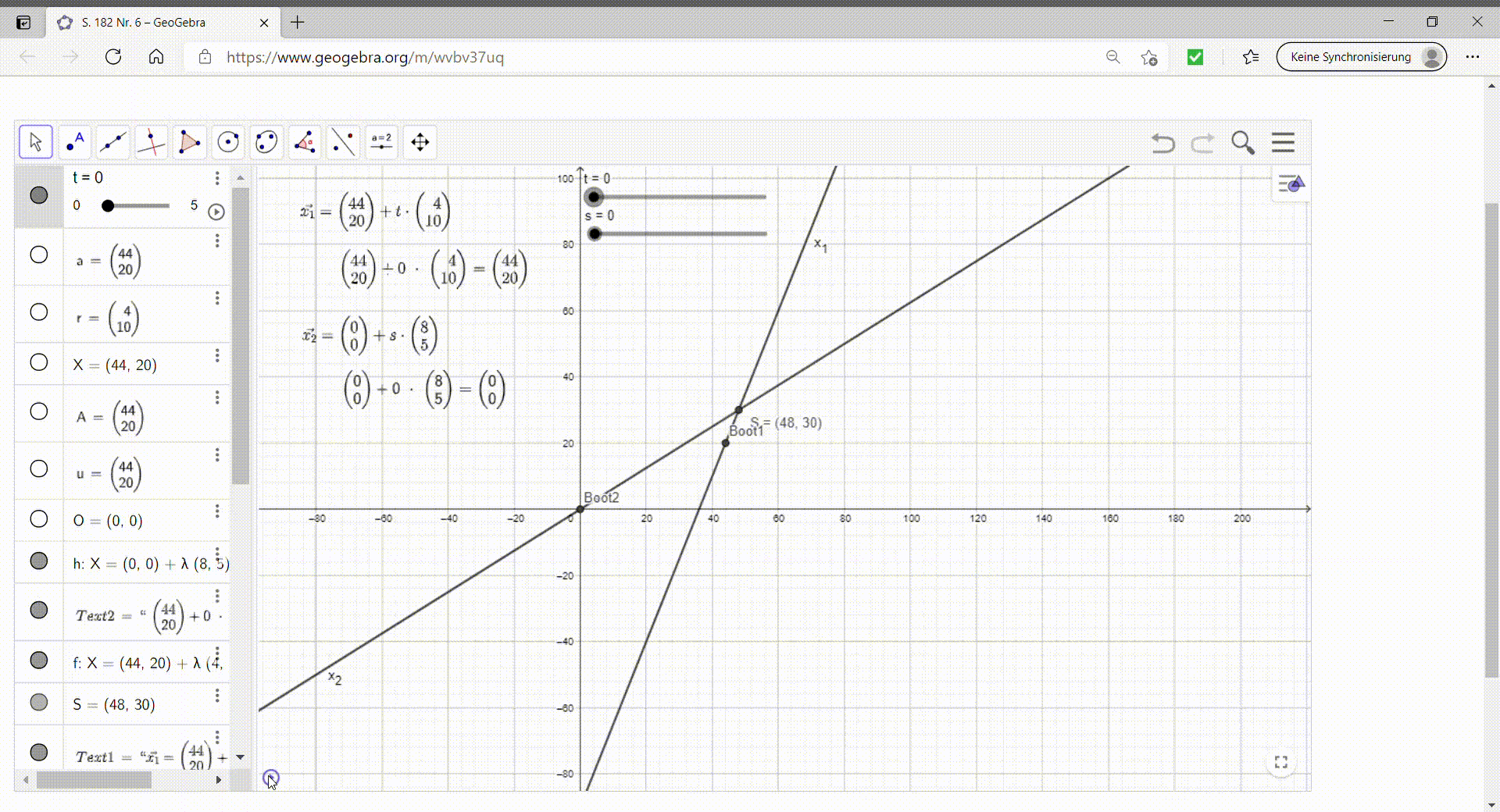
Hier wurde eine Schulbuchaufgabe in GeoGebra visualisert: Obwohl die Geraden als Fahrspuren der beiden Boote sich schneiden, kommt es nicht zu einer Kollision der beiden Wasserfahrzeuge. |
|
GeoGebra in Leistungskurs und Sek I

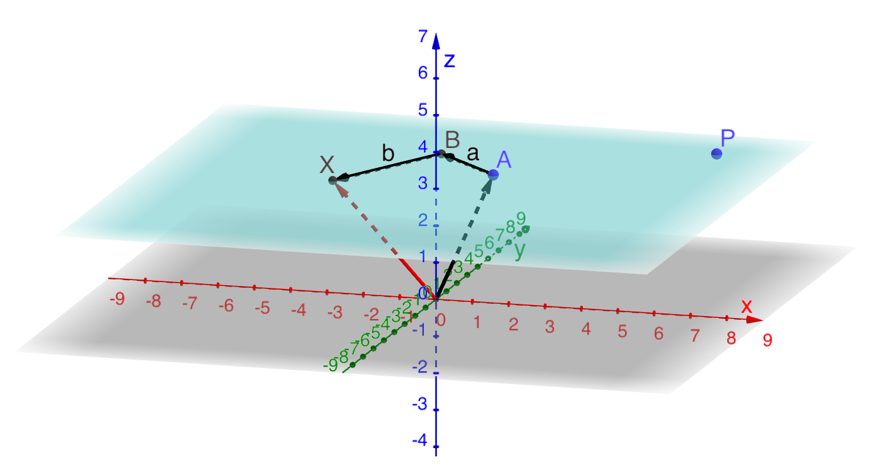
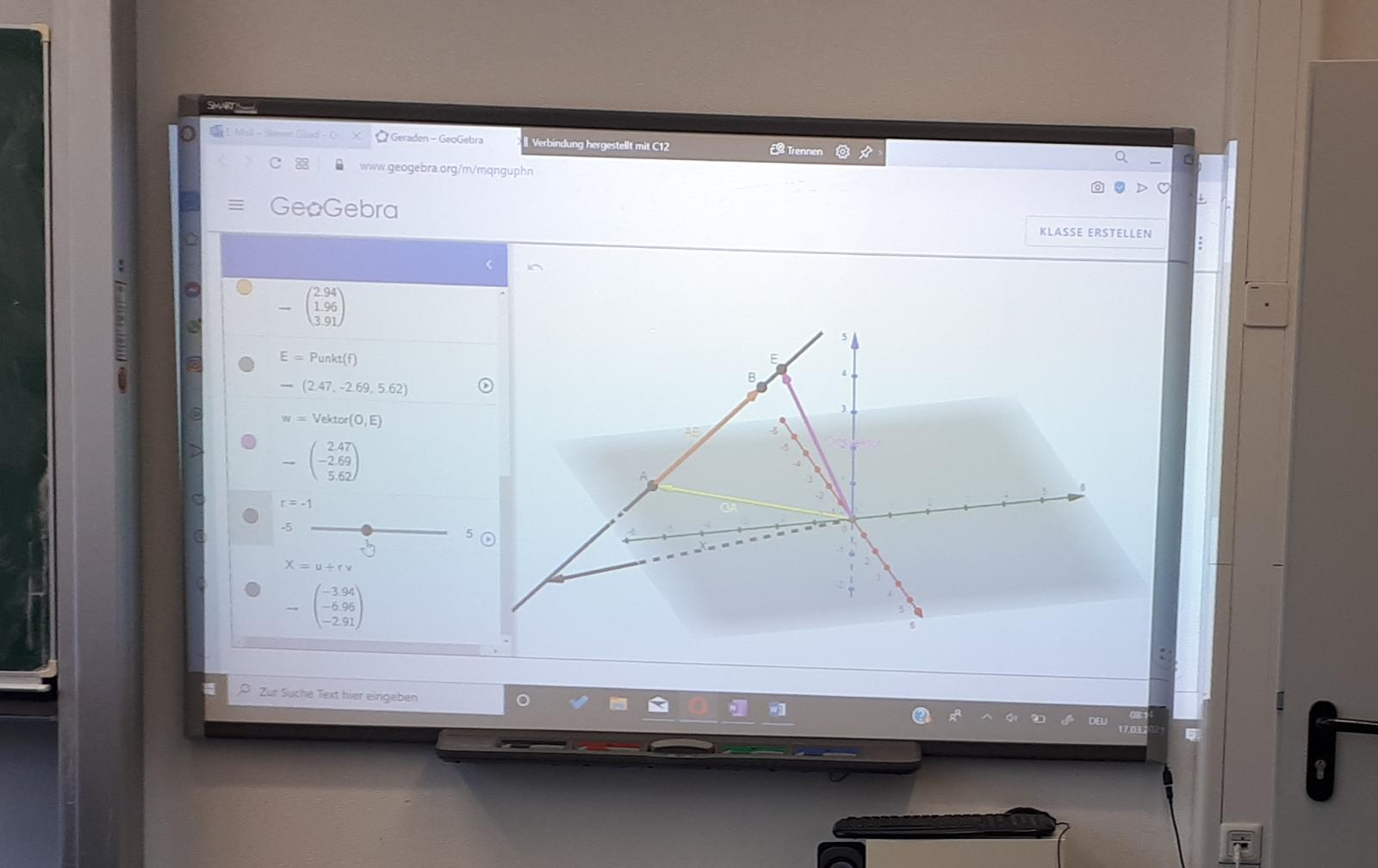 In dem Q1 LK von Herrn Wagener wurden die Geradengleichung mit einem Parameter anhand von GeoGebra anschaulich eingeführt. Dabei handelt es sich hier um ein Applet, womit die Schülerinnen und Schüler herausfinden können, dass durch einfaches Verschieben mit Hilfe eines Schiebereglers für den Parameter, jeder Punkt auf der Geraden erhalten werden kann. Diese Thematik gehört zu dem Inhaltsfeld “analytische Geometrie”. GeoGebra 3D spielt hier eine wichtige Rolle, da durch Visualisierung von Geraden und Vektoren im Raum und die damit verbundene 3D-Ansicht, die Möglichkeit gegeben wird, den Sachverhalt aus verschiedenen Perspektiven zu betrachten, was an einer gewöhnlichen Tafel nicht möglich ist. So kann das Vorstellungsvermögen der Schülerinnen und Schüler gefördert und Raum für besseres Verständnis geschaffen werden. Sowohl Lehrer als auch Lernende waren positiv überrascht von den Möglichkeiten und der schnellen und einfachen Darstellung der Sachverhalte in GeoGebra 3D. “Es ist ziemlich angebracht, das so darzustellen. So kann man sich alles besser vorstellen. Aus dem Kopf heraus kann man sich sowas nicht gut vorstellen, aber mit dieser Abbildung/Darstellung klappt das sehr gut.” (Schüler A). “”Allgemein gut. Jetzt sehen wir endlich die z-Achse, wie sie aussieht bzw. jetzt weiß man, wie man sich die z-Achse vorstellen soll.” (Schüler S). ”Viel leichter zu verstehen und besser nachzuvollziehen.” (Schülerin A). “Durch GeoGebra 3D lassen sich verschiedenen Ansichten darstellen und Anschauungen schaffen. Sehr schön.” (Lehrkraft W).
In dem Q1 LK von Herrn Wagener wurden die Geradengleichung mit einem Parameter anhand von GeoGebra anschaulich eingeführt. Dabei handelt es sich hier um ein Applet, womit die Schülerinnen und Schüler herausfinden können, dass durch einfaches Verschieben mit Hilfe eines Schiebereglers für den Parameter, jeder Punkt auf der Geraden erhalten werden kann. Diese Thematik gehört zu dem Inhaltsfeld “analytische Geometrie”. GeoGebra 3D spielt hier eine wichtige Rolle, da durch Visualisierung von Geraden und Vektoren im Raum und die damit verbundene 3D-Ansicht, die Möglichkeit gegeben wird, den Sachverhalt aus verschiedenen Perspektiven zu betrachten, was an einer gewöhnlichen Tafel nicht möglich ist. So kann das Vorstellungsvermögen der Schülerinnen und Schüler gefördert und Raum für besseres Verständnis geschaffen werden. Sowohl Lehrer als auch Lernende waren positiv überrascht von den Möglichkeiten und der schnellen und einfachen Darstellung der Sachverhalte in GeoGebra 3D. “Es ist ziemlich angebracht, das so darzustellen. So kann man sich alles besser vorstellen. Aus dem Kopf heraus kann man sich sowas nicht gut vorstellen, aber mit dieser Abbildung/Darstellung klappt das sehr gut.” (Schüler A). “”Allgemein gut. Jetzt sehen wir endlich die z-Achse, wie sie aussieht bzw. jetzt weiß man, wie man sich die z-Achse vorstellen soll.” (Schüler S). ”Viel leichter zu verstehen und besser nachzuvollziehen.” (Schülerin A). “Durch GeoGebra 3D lassen sich verschiedenen Ansichten darstellen und Anschauungen schaffen. Sehr schön.” (Lehrkraft W).
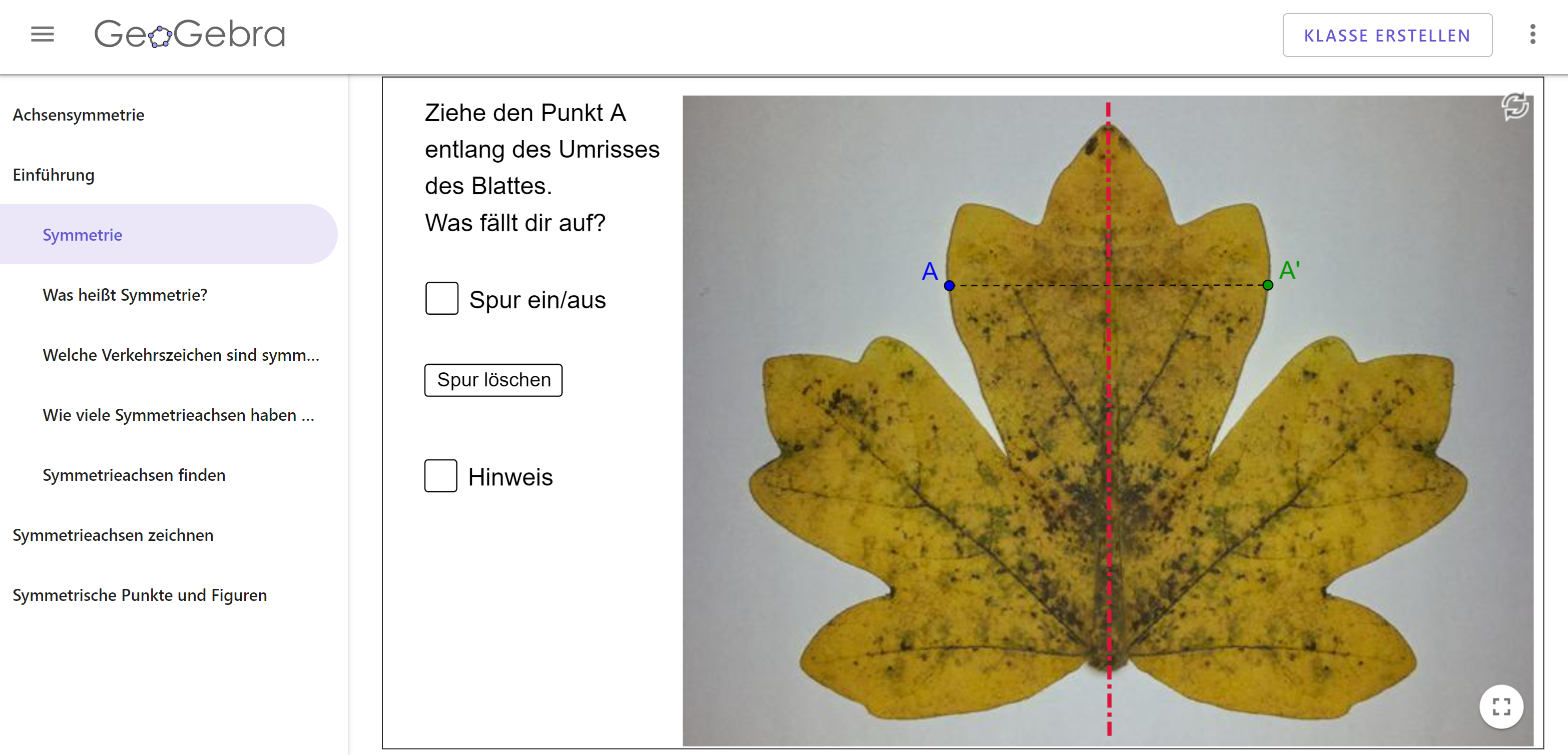
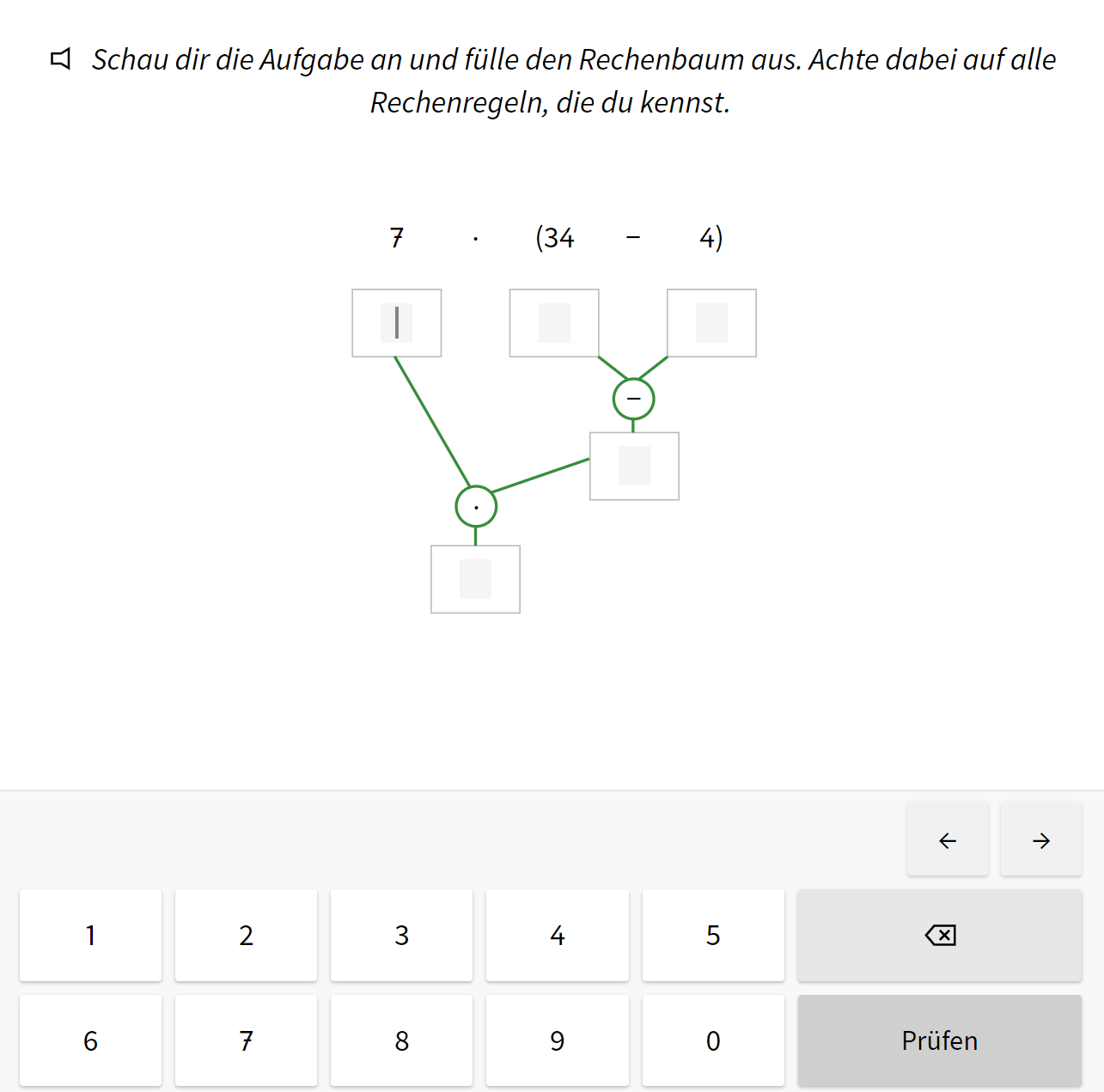 In der 5. Klasse wurde die Anton-App eingeführt, welche nicht nur im Distanzunterricht, sondern auch im Präsenzunterricht genutzt werden kann. Die Anton-App dient zum selbstständigen und spielerischen Üben mit Kontrolllösungen. Dabei kann die Lehrkraft selbst den Lernfortschritt der Schülerinnen und Schüler beobachten und Probleme schnell erkennen und entgegenwirken. Besonders im Distanzunterricht, wo die Kontrolle von Aufgaben und das damit verbundene Verständnis zu überprüfen erschwert ist, bietet die Anton-App eine gute Möglichkeit. Dieses Programm wurde bisher in den Bereichen des Rechnens (Arithmetik) und der Symmetrie (Geometrie) genutzt. Vor allem die Schülerinnen und Schüler haben sehr viel Freude an der Anton-App “Das macht Spaß!”. “Darf ich weiter mit der Anton-App arbeiten?”.
In der 5. Klasse wurde die Anton-App eingeführt, welche nicht nur im Distanzunterricht, sondern auch im Präsenzunterricht genutzt werden kann. Die Anton-App dient zum selbstständigen und spielerischen Üben mit Kontrolllösungen. Dabei kann die Lehrkraft selbst den Lernfortschritt der Schülerinnen und Schüler beobachten und Probleme schnell erkennen und entgegenwirken. Besonders im Distanzunterricht, wo die Kontrolle von Aufgaben und das damit verbundene Verständnis zu überprüfen erschwert ist, bietet die Anton-App eine gute Möglichkeit. Dieses Programm wurde bisher in den Bereichen des Rechnens (Arithmetik) und der Symmetrie (Geometrie) genutzt. Vor allem die Schülerinnen und Schüler haben sehr viel Freude an der Anton-App “Das macht Spaß!”. “Darf ich weiter mit der Anton-App arbeiten?”.
Aber auch GeoGebra ist ein gutes digitales Medium, welches die 5. Klasse bereits nutzt. Hier wurde die Achsensymmetrie (Inhaltsfeld der Geometrie) bereits anhand von Applets nähergebracht. Die Schülerinnen und Schüler können so gewisse Eigenschaften besser und sogar schneller verinnerlichen und haben gleichzeitig eine schöne Anschauung, welche die visuelle Ebene von Aufgaben stützt. Ebenso bietet GeoGebra die Möglichkeit, dass sich die Lernenden selbst kontrollieren und so eine direkte Rückmeldung über die Richtigkeit bekommen. Schülerinnen und Schüler reagieren hierbei positiv “Das ist ja wie als wenn man einen Spiegel an die Spiegelachse hält”. GeoGebra hat dabei auch etwas Spielerisches an sich, wodurch die Schülerinnen und Schüler gerne selbst ausprobieren und selbständig anfangen zu arbeiten.