Zeitungen und Zahlen, oder: Deutschland als Anumeriker-Land

Früher dachte ich immer, es sei nur ein Problem meiner Lieblingstageszeitung. Meine Lieblingstageszeitung bringt die besten Titelseiten unter aller Zeitungen Deutschlands, hat die besten Fußballberichte (wenn auch viel zu wenige derselben – wie überhaupt diese Zeitung vergleichsweise dünn ist), sie versucht, ihre Kulturberichterstattung aufzupäppeln (wenn auch mit wenig Erfolg), und ist ständig im Kampf um ihre Existenz. Wie sollte da also Zeit bleiben, sich um Zahlen zu kümmern? Da kann man "billions" schon mal als "Billionen" eindeutschen – egal; man kann Rechenexempel bringen, bei denen schon Kindergartenkinder merken, dass sie nicht stimmen – sind ja eh nur Zahlen.

Es ist aber nicht nur ein Problem meiner Lieblingstageszeitung. Nein, auch bei Zeitungen, die sich als überregionale Meinungsführer gerieren, passieren Dinge, die einem Kind in der zweiten Grundschulklasse die Schamesröte ins Gesicht treiben würden. Hat man aber schon mal erlebt, dass sich eine Zeitung für den Schmuh entschuldigen würde, den sie den Leserinnen und Lesern vorsetzt? (Ähm, ja, doch, gerade bei meiner Lieblingstageszeitung ist das in letzter Zeit hin und wieder vorgekommen. Danke und nix für ungut.)

Die folgenden Beispiele sind ganz unsystematisch zusammengesammelt. Und werden der Einfachheit halber chronologisch und nicht sachlich geordnet. Es handelt sich nur um eine kleine und ganz willkürliche Auswahl, weil ich weder viel Zeitung lese noch Lust habe, jedes Mal hier einen Eintrag zu machen, wenn mir wieder ein Beispiel inkompetenten Umgangs mit Zahlen über den Weg läuft.

Künstliche Intelligenz und natürliche Dummheit (DIE ZEIT Nr. 43, 2019, S. 41)

Im Herbst 2019 hat sich eine Reporterin der ZEIT mit der finnischen nationalen KI-Strategie befasst; danach soll ein Prozent der Bevölkerung anhand eines Online-Kurses Kenntnisse über KI erwerben. Die Reporterin hat sich selbst durch den Kurs gearbeitet. Was sie davon berichtet, wäre besser nicht gedruckt worden.

Ein Teil des Kurses befasst sich mit Wahrscheinlichkeitsrechnung, und die Reporterin beschreibt eine Aufgabe und ihre Lösung (für die sie angeblich vom System gelobt wurde). Die Aufgabe: Ich wache am Morgen auf und es sind Wolken am Himmel. Wie wahrscheinlich ist es, dass es heute regnet? Dafür bekomme ich zwei Informationen:

• Es regnet im Schnitt an 206 Tagen im Jahr;
• an neun von zehn Regentagen gibt es morgens Wolken am Himmel.

Was macht die Reporterin daraus? Im ZEIT-Blog haben sich zu Recht mehrere Leserbriefschreiber darüber geärgert, dass die Reporterin aus den genannten Angaben folgende ‚Wahrscheinlichkeiten‘ errechnet: Die (unbedingte) Wahrscheinlichkeit, dass es regnet, betrage 206:159 und die (bedingte) Wahrscheinlichkeit, dass es an einem Regentag morgens Wolken am Himmel gibt, wird als 9:1 angegeben. Die Zahlen sind nicht mal falsch – aber es sind keine Wahrscheinlichkeiten, sondern sog. Odds oder ‚Gewinnchancen‘. Die Wahrscheinlichkeit, dass es regnet, errechnet sich als 206:365 (dazu kann man die einfachste Grundlage der Wahrscheinlichkeitslehre heranziehen, den Satz von Laplace); grundsätzlich haben Wahrscheinlichkeiten immer Werte zwischen 0 und 1.

Aber das ist nicht das eigentliche Problem des Artikels, denn schließlich können alle, die wollen, aus den Angaben (oder auch aus den Odds!) die Wahrscheinlichkeiten selbst errechnen. Nein, wirklich falsch wird es erst im Folgenden: Die Autorin multipliziert einfach die beiden ‚Wahrscheinlichkeiten‘ (also die Odds) und stellt das Ergebnis – 1854:159 – als die Wahrscheinlichkeit dar, dass es an dem betreffenden Tag regnen wird. Das ist ganz unabhängig von der falschen Grundlage der Berechnung (Odds statt Wahrscheinlichkeiten) leider Nonsense.

Dazu muss man sich Folgendes überlegen: Wenn ich weiß, dass es an 206 Tagen im Jahr regnet und dass an 90 Prozent dieser Regentage morgens Wolken am Himmel stehen, dann weiß ich erst einmal nur, dass sich die 206 Regentage auf 185,4 Tage mit morgendlichen Wolken und 20,6 Tage ohne morgendliche Wolken verteilen. Ich kann also sagen: Meistens gibt es Wolken, wenn es später regnet. Was ich wissen will, ist aber etwas anders: Wie oft gibt es Regen, wenn morgens Wolken am Himmel sind? Um das zu errechnen, muss ich auch wissen, wie groß die Wahrscheinlichkeit von Wolken an den übrigen 159 Tagen ist (oder, im Lichte der bereits vorliegenden Informationen: wieviele Wolkentage es insgesamt pro Jahr gibt). Wenn an den Tagen ohne Regen niemals morgens Wolken am Himmel stehen, dann sind die Wolken, die ich heute sehe, äußert informativ: Sie deuten auf eine hohe Wahrscheinlichkeit des Regnens hin. Es könnte aber auch sein, dass an Tagen ohne Regen grundsätzlich immer morgens Wolken zu sehen sind. Dann wüsste ich zum einen, dass es eigentlich fast immer morgens bewölkt ist – und weiterhin, dass die Wolken für eine im Vergleich zum Durchschnitt leicht verringerte Regenwahrscheinlichkeit stehen. Aber die Wahrheit liegt sicherlich irgendwo dazwischen.

Jedenfalls ist klar: Ich muss beide bedingte Wahrscheinlichkeiten kennen: die, dass es Wolken an Regentagen gibt, ebenso wie die, dass es Wolken an Tagen ohne Regen gibt. Wie man dann die gewünschte Wahrscheinlichkeit errechnet, sagt uns der Satz von Bayes.

Kaugummis verseuchen die Welt (DIE ZEIT Nr. 15 und Nr. 16 2016, Infografik)

375 Trillionen Kaugummistreifen werden jährlich hergestellt, berichtet die Infografik im Wissen-Teil der ZEIT Nr. 15. Eine beachtliche Menge, doch eine Woche später folgt die Korrektur: Es sind nur 375 Billionen.

Nur: Was passiert denn mit all diesen Streifen? Wie man unschwer erkennen kann, sind das immer noch eine gute Billion Streifen pro Tag. Und das bei einer Erdbevölkerung von 7,4 Mrd. Menschen! Macht grob überschlagen 135 bis 140 Kaugummistreifen pro Person und Tag – und noch nicht eingerechnet ist, dass ein substanzieller Teil der Bevölkerung weltweit kaugummiabstinent sein dürfte. Werden die Kaugummis vielleicht an Ameisen und Termiten verfüttert? Oder an wen sonst?

Gucken wir die Infografiken weiter an: 560.000 Tonnen Kaugummi sollen jährlich gekaut werden (ZEIT Nr. 15). Wenn wir mal annehmen, dass dies in etwa den oben erwähnten 375 Billionen Streifen entspricht – dann wiegt ein Streifen ca. 670 g, über ein Pfund. Ich habe schon seit ein paar Jahrzehnten keinen Kaugummi mehr gekauft, aber beim letzten Mal waren die Dinger etwas leichter ...

Viel Geld für Kinder (DIE ZEIT Nr. 27 vom 28.06.2012, S. 3)

Nicht nur für das Gesundheitswesen (siehe folgenden Eintrag), auch für Kinder hat Deutschland viel Geld übrig:

»Nach einer Untersuchung der Organisation für wirtschaftliche Zusammenarbeit und Entwicklung (OECD) liegen die öffentlichen Ausgaben pro Kind hierzulande bei 146 000 Euro pro Jahr – im OECD-Durchschnitt sind es 22 000 Euro weniger.«

146 000 Euro pro Jahr und Kind ... hm. Gut, wir wissen nicht genau, was hier mit »Kind« gemeint ist; der Artikel geht vor allem über die Kita-Plätze der unter 3-jährigen. Nehmen wir einfach mal an, dass die Zahlen sich auf diese Gruppe beziehen, die in Deutschland gut zwei Millionen Kinder umfasst. Alleine für drei Altersjahrgänge gibt also Deutschland pro Jahr grob überschlagen 300 Mrd. Euro aus, mehr als 10 Prozent des Bruttoinlandprodukts. Respekt! Zumal ja sicher für die anderen Jahrgänge (die im übrigen mehr Kinder umfassen) auch noch etwas Geld aufgewendet wird.

Einmal mehr der Tipp: Beim Hinschreiben (oder Durchlesen) einfach nochmal kurz innehalten und nachdenken! Und dann recherchieren: Ich habe drei Minuten gebraucht, um den Bericht zu finden (Doing Better for Families, Deutschland): Es geht um 146 000 Euro für die gesamte Zeit bis zum 18. Lebensjahr eines Kindes. Aber fünf Minuten Zeit hat man bei der ZEIT wohl nicht mehr.

Teures Gesundheitssystem (DIE ZEIT Nr. 48 vom 25.11.2010, S. 38)

Folgendes lesen wir unter der Überschrift »Womit der Apotheker sein Geld verdient«:

»Die Apotheken in Deutschland erzielten im Jahr 2009 insgesamt einen Umsatz von 39,2 Milliarden Euro ... Auf Apotheken entfallen somit 2,6 Prozent der Ausgaben der gesetzlichen Krankenkassen.«

Stimmte das, so hieße es: Die Gesamtausgaben der gesetzlichen Krankenkassen betrugen im Jahr 2009 1.507,7 Mrd. Euro. Bei einem Bruttoinlandsprodukt von 2.397,1 Mrd. Euro im Jahr 2009 also über 60 Prozent des BIP nur für die gesetzliche Krankenversicherung! Da kann man doch nur in tiefste Ehrfurcht vor dem Gesundheitsminister versinken, der es bislang erfolgreich verstanden hat, diese Tatsache nicht publik werden zu lassen.

Oder ... hat da mal wieder jemand beim Rechnen nicht aufgepasst?

Elementare Statistik – leider nicht aufgepasst (DIE ZEIT Nr. 45 vom 3.11.2005, S. 67)

Das Wochenblatt berichtet von einem interessanten Befund zu den Auswirkungen von Preiserhöhungen bei Zigaretten:

"Michael Grossman, ein Ökonom an der City University von New York, kalkuliert: Wenn der Zigarettenpreis um zehn Prozent steigt, wächst die Zahl der Fettleibigen um zwei Prozent. In Statistikerkreisen gilt derlei als ziemlich gute Korrelation."

Der Autor, immerhin Josef Joffe, einer der Herausgeber der ZEIT, kennt sich in diesen Kreisen ganz offensichtlich entgegen seiner Insinuation – der Satz suggeriert, er würde regelmäßig in diesen Kreisen verkehren – nicht aus, denn tatsächlich würde man einem Statistiker, der so etwas behauptet, sein Diplom entziehen. Nicht weil es sich hierbei etwa um eine "schlechte Korrelation" handelte, sondern weil das, was Herr Joffe bei Grossman (immerhin richtig) gelesen hat, nichts, nichts und wieder nichts über die Stärke eines Zusammenhanges aussagt – und nur das kann ja mit "gute Korrelation" gemeint sein –, sondern ausschließlich über dessen Richtung (genauer: über den Steigungskoeffizienten einer Regressionsgeraden bzw. -ebenen). Den Unterschied verdeutlichen exemplarisch die beiden folgenden Graphiken, die beide einen richtungsmäßig (ungefähr) gleichen Zusammenhang, aber von deutlich unterschiedlicher Stärke, darstellen: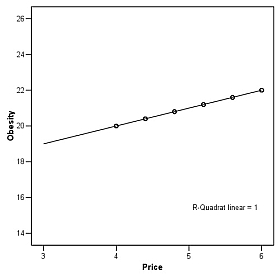

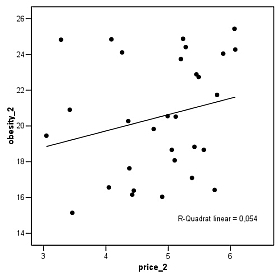
Im ersten Fall liegen alle Datenwerte auf einer Geraden; hier besteht ein perfekter Zusammenhang zwischen den beiden Größen. Im zweiten Fall streuen die Datenwerte sehr stark um die Gerade (die gleichwohl die beste Annäherung an den durch die Punktewolke gebildeten Zusammenhang darstellt); die Korrelation beträgt gerade 0,23, was "in Statistikerkreisen" bestenfalls als mäßiger Zusammenhang gilt. Die Angabe der Steigung der Geraden sagt aber offenbar nichts darüber aus, welche der beiden gezeigten (oder vielen anderen möglichen) Konstellationen gegeben ist.

(Für Interessierte: Grossman selbst schreibt [in "The Economics of Obesity", The Public Interest 2004, zusammen mit Inas Rashad], dass die Preiserhöhungen fast 20 Prozent des Anstiegs der Fettleibigkeit erklären. Das ist ein einigermaßen starker Zusammenhang, er entspricht einer Korrelation von 0,45. Tatsächlich wird man "in Statistikerkreisen" in diesem Kontext gar nicht von Korrelation sprechen, sondern von "erklärter Varianz"; aber da man nicht vermuten kann, dass dieser technische Ausdruck einem breiten Publikum geläufig ist, scheint mir die Annäherung durch den Begriff Korrelation durchaus vertretbar. Was allerdings Joffe [und auch Grossman in seinem Artikel] gar nicht diskutieren, ist das Thema "ökologischer Fehlschluss"; auch hierzu befrage man eine einschlägige Quelle zu sozialwissenschaftlichen Forschungsmethoden.)

Vergreistes Halle? (DIE ZEIT Nr. 40 vom 29.9.2005, S. 69)

Dass die Bevölkerungsstruktur Deutschlands sich in den nächsten Dekaden dramatisch ändern wird, ist bekannt. Wie dramatisch es zugehen wird, weiß allein die ZEIT:

"Und wenn dann auch noch vom Statistischen Landesamt die Mitteilung kommt, dass im Jahr 2020 rund 80 Prozent aller Einwohner von Halle [an der Saale, Anm. WL-M] außerhalb regulärer Erwerbstätigkeit stehen werden – weil sie dann entweder unter 20 oder über 65 Jahre alt sind? Niemand hat heute eine Vorstellung davon, wie eine Stadt mit einem solchen Bevölkerungsschema funktionieren könnte."

Ebenso wie niemand eine Vorstellung davon hat, wie einer, dem nicht spätestens beim Hinschreiben solcher Zahlen deren Unstimmigkeit auffällt, bei einem angeblich so distinguierten Organ wie der ZEIT landen kann. Die vom Statistischen Landesamt Sachsen-Anhalt veröffentlichte "3. Regionalisierte Bevölkerungsprognose 2002 bis 2020" sagt uns denn auch etwas ganz Anderes: dass im Jahr 2020 der Anteil der genannten Altersgruppen (unter 20/über 65) 80 Prozent des Anteils der mittleren Altersgruppe ausmachen wird. Anders gesagt: Die ganz Jungen und die ganz Alten werden immer noch die Minderheit der Einwohner Halles darstellen, eine große Minderheit, gewiss, aber das ist doch etwas Anderes als die vom Autor herbeiphantasierte Vision einer vierfachen numerischen Überlegenheit.

Prozent oder Promille? (taz Nr. 7318 vom 25. März 2004)

Die Fettleibigkeit bei amerikanischen Kindern ist gestiegen, doch würde es Kindern in den USA nicht durchgängig schlechter gehen, schreibt die taz auf S. 2: "Waren 1974 noch 77,5 Prozent von 1.000 Kindern zwischen 12 und 15 Jahren in Gefahr, Opfer eines Gewaltverbrechens zu werden, waren es 2002 noch 44,4 Prozent."

Hm, 77,5 Prozent ist schon verdammt viel. Und warum steht da eigentlich 77,5 Prozent von 1.000 Kindern? Also suchen wir mal schnell im Internet und lesen den gleichen (auf AP zurückgehenden) Bericht in der Version von Canada Press:

"The report noted that 44.4 of every 1,000 people between the ages of 12 and 15 were likely to be victims of violent crime in 2002, down from 77.5 per 1,000 in 1974".

(Nur nebenbei: 44,4 Kinder unter 1000 waren nicht in Gefahr, wie die taz schreibt, Opfer eines Gewaltdelikts zu werden, sondern sie wurden Opfer von Gewaltdelikten. Der Canadian Press-Bericht verschleiert dies allerdings auch etwas ["were likely to ..."], aber das geht vermutlich auf die – mir nicht zugängliche – Originalquelle zurück: Wissenschaftler setzen Wahrscheinlichkeiten oft mit realisierten Häufigkeiten gleich, was freilich im konkreten Fall nicht sinnvoll ist, sondern nur dann, wenn wir uns einen sog. "Zufallsvorgang", etwa das Werfen eines Würfels, unendlich oft wiederholt denken.)

Frauen = Professoren = Dicke = Sportmuffel (taz Nr. 7275 vom 4. Februar 2004, S. 7)

Eng verwandt mit der Malträtierung von Zahlen ist die von Relationen, Proportionen usw. Hier mal ein Beispiel für Relationen, schon wieder aus meiner Lieblingstageszeitung:

"Frauen wollen wie Professoren zahlen"

geht die Überschrift eines Artikels, und die ist noch korrekt: Frauen beklagen sich, dass sie wegen höherer Lebenserwartung bei der Riester-Rente mehr zahlen müssen als Männer, um die gleiche Rente zu erzielen wie diese. Das sei ungerecht, denn auch Professoren hätten eine hohe Lebenserwartung, müssten aber nicht mehr zahlen als andere Männer. Also, fährt die Zeitung fort: "Wollte man die vermutete Lebensdauer gewichten, müsste der Professor mehr zahlen als der Möbelpacker, der Dicke mehr als der Dünne, der Sportmuffel mehr als der Fitness-Freak."

Wir verstehen: Frauen haben eine längere Lebenserwartung als Männer, Professoren eine längere als Möbelpacker, Dicke eine längere als Dünne, Sportmuffel mehr als Sport treibende. Rasch auf die Waage – nur 81 Kilo. Das reicht noch nicht, also ab ins Wirtshaus zur Schweinshaxn.

Schneller reich werden mit der SZ (Nr. 7 vom 10./11. Januar 2004, S. V1/11)

"Man könne von einem 'Return on Investment' von knapp fünf Prozent ausgehen: Wer 100 000 Euro investiere, erhalte 120 000 Euro zurück".

So schreibt die Zeitung über Gesundheitsinitiativen in Firmen. Darf ich damit jetzt zu meiner Bank gehen, die mir fünf Prozent Rendite versprochen hat, und für 1000 investierte Euro (100 000 sind bei mir natürlich nicht drin ...) 1200 Euro zurückverlangen?

die tageszeitung, Nr. 7253 vom 9.1.2004

Hier mal ein Beispiel, ausnahmsweise aus meiner Lieblingstageszeitung, für eine Zahl, die nicht falsch ist, aber bei der eine entscheidende Kontextinformation fehlt:

"Und auch die 400-Milliarden-Subventionierung der Medikamentenkosten von Senioren war kein kleiner Wurf" (S. 3 über George W. Bush)

400 Mrd. US-Dollar, hmmm ... auch für die USA kein kleiner Batzen, noch dazu wenn wir weiter unten lesen, dass das aktuelle Haushaltsdefizit gerade mal 500 Mrd. beträgt. Also recherchieren wir ein wenig ... und finden dann heraus, dass es sich bei der Summe von 400 Mrd. um die geschätzten Kosten für die kommenden zehn Jahre handelt! Auch nicht wenig, aber jedenfalls haben wir jetzt eine Zahl mit Kontext, mit der wir etwas anfangen können.

SZ Nr. 293 vom 20./21.12.2003

822 Euro Mehrbelastung pro Jahr errechnet die Zeitung an prominenter Stelle, in einem Kasten auf S. 2, als Beispiel für die Folgen der gerade verabschiedeten Steuerreform für einen "Verheirateten Durchschnittsverdiener mit 2 Kindern, der täglich weit zur Arbeit fährt". Wie das? Ganz einfach:

• Einkommenssteuer sinkt von 4494 Euro auf 4076 Euro.
• Eigenheimzulage sinkt von 1556 auf 1250 Euro
• Kinderzuschlag erhöht sich von 767 auf 800 Euro.

SZ Nr. 251 vom 31.10./1.11./2.11.2003

"Im Geldbeutel zehn Prozent mehr", jubelt die gleiche Zeitung ca. 6 Wochen vorher in einer Überschrift, gefolgt von der Erläuterung: "Was dem Bürger ein Vorziehen der Steuerreform bringen würde". Fein, freut sich das Professorenherz, das ist doch gar nicht so wenig. Wenn es nur stimmte. Lesen wir doch mal das Kleingedruckte (sprich den Text des Artikels):

"Laut Finanzministerium würden die Bürger im Schnitt zehn Prozent weniger Einkommenssteuer zahlen."

PS: Manchmal habe ich so einen Gedanken, den ich ganz schnell wieder wegschiebe: Wie, wenn die demonstrierte Inkompetenz der Zeitungen sich nicht nur auf das Gebiet der Zahlen beschränkte?