Idee der empirischen Theorien im Mathematikunterricht
Basis für die Forschungsarbeit ist die Idee der Relevanz von Auffassungen von Mathematik für die Entwicklung und Vermittlung mathematischen Wissens. Neben vielfältigen Ergebnissen aus der deutschen „Beliefsforschung“ beziehen wir uns auf die Arbeiten von Struve (z.B. 2010 mit Burscheid) sowie von Schoenfeld (1985 & 2011) und Tall (2013). Bei Schoenfeld (1985, S. 45) heißt es dazu als Folge von grundlegenden empirischen Studien und theoretischen Überlegungen,
“Belief systems are one’s mathematical world view, the perspective with which one approaches mathematics and mathematical tasks. One’s beliefs about mathematics can determine how one chooses to approach a problem, which techniques will be used or avoided, how long and how hard one will work on it, and so on. Beliefs establish the context within which resources, heuristics, and control operate.”
Schoenfeld zeigt, dass Schülerinnen und Schüler im Mathematikunterricht ein „empirical belief system“ (d.h. frei übersetzt eine „naturwissenschaftliche Auffassung“) von Mathematik erwerben.
Die Beobachtung, dass Schülerinnen und Schüler im Unterricht Theorien über reale Phänomene erwerben, in diesem Sinne also mit einem Begriff der Wissenschaftstheorie („Strukturalismus“ nach Balzer, Moulines, Sneed, Stegmüller) empirische Theorien lernen, wird auch durch kognitionspsychologische Untersuchungen gestützt. Die Entwicklungspsychologin Gopnik formuliert dazu, dass
„[…] sich Kinder die Welt in ganz ähnlicher Weise wie Naturwissenschaftler [aneignen]: Sie experimentieren gezielt, bewerten gewonnene statistische Muster und stellen anhand ihrer Beobachtungen Theorien auf“ (Gopnik 2010, S. 69).
Die im Schulunterricht erworbene empirische Auffassung von Mathematik ist auf erkenntnistheoretischer Ebene betrachtet keine defizitäre, sondern eine angemessene wie ich u.a. in meiner Dissertationsschrift „Die Entwicklung des leibnizschen Calculus, eine Fallstudie zur Theorieentwicklung in der Mathematik“ zeigen konnte. Dabei ist es möglich, auf erkenntnistheoretischer Ebene Entwicklungsgesetzmäßigkeiten zu identifizieren, die Entsprechungen in unterrichtlicher Entwicklung von mathematischem Wissen haben.
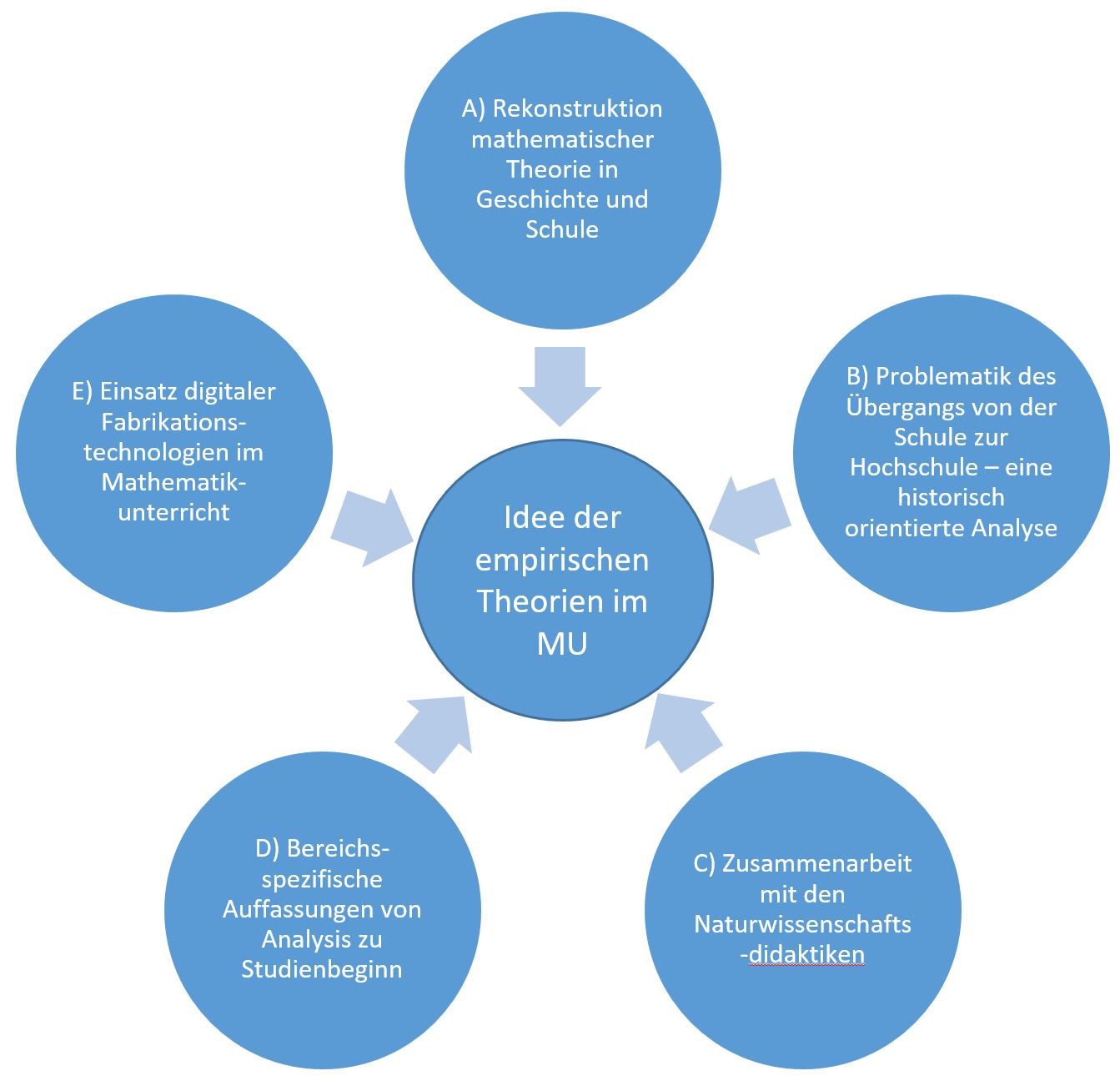
Die Idee, das Verhalten von Schülerinnen und Schülern im Mathematikunterricht im Sinne von empirischen Theorien (auf verschiedenen Ebenen) zu erforschen, bietet den wesentlichen Ausgangspunkt für meine weitere Forschungsarbeit
Weitere Informationen zu den übrigen Forschungsfeldern finden Sie unter den nachfolgenden Links:
- A) Rekonstruktion der Entwicklung mathematischen Wissens in Geschichte und Schule
- B) Übergangsproblematik Schule - Hochschule
- C) Erkenntnistheoretische Parallelen Mathematik-Naturwissenschaften
- D) Schüler/Studierendenauffassungen von Analysis
- E) MINTUS-Digital
Literatur
Burscheid, Hans Joachim; Struve, Horst (2010): Mathematikdidaktik in Rekonstruktionen. Ein Beitrag zu ihrer Grundlegung. Hildesheim: Franzbecker.
Schoenfeld, Alan H. (1985): Mathematical Problem Solving. Orlando et al.: Academic Press.
Schoenfeld, Alan H. (2011): How We Think. In: Studies in Mathematical Thinking and Learning. New York York et al.: Routledge.
Tall, David. (2013): How Humans Learn to Think Mathematically. Exploring the three worlds of mathematics. New York: Cambridge University Press.