C) Erkenntnistheoretische Parallelen Mathematik-Naturwissenschaften

 

 

 

Aus der im Abschnitt Idee der empirischen Theorien im MU beschriebenen Auffassung von Mathematik, insbesondere ihrer engen ontologischen Bindung aus Sicht der Schülerinnen und Schüler, ergibt sich eine natürliche Verbindung zu den Naturwissenschaften. Sind die intendierten Anwendungen einer schulmathematischen Theorie gegenstandsbezogen – z.B. bei einer Analysis auf Grundlage von Kurven, einer Bruchrechnung auf Grundlage von Tortenmodellen oder einer Wahrscheinlichkeitsrechnung auf Grundlage von Würfelexperimenten – so sind erkenntnistheoretische Parallelen zu den experimentellen Naturwissenschaften gegeben; d.h., anders als in formaler Hochschulmathematik, aber vergleichbar mit den Naturwissenschaften, ist z.B. Wissenssicherung im Experiment wesentlicher Bestandteil sogenannter empirischer Mathematik (Burscheid & Struve 2010, Philipp 2013). Tall (2013) beschreibt ein ähnliches Phänomen wenn er von conceptual embodiement im Zusammenhang von practical mathematics spricht. Auch die Existenz von nicht-theoretischen Begriffen (also solchen mit gegenständlichem Referenzobjekt) und theoretischen Begriffe (also solchen ohne Referenzobjekt) begründet dann bemerkenswerte erkenntnistheoretische Parallelen. Diese Parallelen zu erforschen erscheint mit Blick auf den modernen Mathematikunterricht und den Schwierigkeiten, die dem Erwerb theoretischer Begriffe (Wahrscheinlichkeitsbegriff, Grenzwertbegriff, Ableitungsbegriff, Zahl Null) inne liegt, dringend geboten. So besteht z.B. in der Physik im Bereich der Newton’schen Mechanik ein auf erkenntnistheoretischer Ebene paralleler Problembereich mit Begriffen wie Kraft und Masse.

Zusammenhänge dieser Art bilden die Grundlage für die erste Forschungslinie im neugegründeten Forschungsverbund MINTUS an der Universität Siegen. Hier haben sich die beteiligten Didaktiken (Mathematikdidaktik, Physikdidaktik, Chemiedidaktik und Technikdidaktik) darauf verständigt im ersten Durchlauf die „Rolle, Aufgabe und Funktion von Mathematik“ in den MINT-Fächern zu untersuchen. Für die Ausgestaltung der einzelnen geplanten interdisziplinären Teilprojekte mit der Physik- und der Technikdidaktik vgl. MINTUS-Sti’MINT. Hier verortet sich auch das Dissertationsprojekt von Kathrin Holten, die ausgehend von empirischen Erhebungen aus Lehramtsseminaren und einer vergleichenden Schulbuchanalyse Parallelen hinsichtlich des Zuganges zum Ableitungsbegriff zwischen der Mathematik und den naturwissenschaftlichen Fächern in der Schule ergründet.

Das dazu konzipierte Lehr- und Forschungsprojekt („FäMaPdi“ = fächerverbindende Mathematik und Physikdidaktik“) läuft seit dem Wintersemester 2014/2015 mit Prof. Schwarz (Physikdidaktik) in Siegen. An dem Projekt sind vier Wissenschaftler aus der Mathematikdidaktik und der Physikdidaktik sowie das Zentrum für Bildungsforschung beteiligt. Um die schulische Perspektive authentisch einzubringen ist außerdem ein erfahrener Lehrer in das Projekt eingebunden. Das Projekt zeichnet sich dadurch aus, das Studierende im Rahmen von forschendem Lernen fächerverbindende Unterrichtsentwürfe entwickeln und in der Schule erproben können.

Mithilfe des Projekts soll der „Praxisschock“ für die Studierenden im Bereich der Sekundarstufen abgemildert, aber auch ein forschend-reflexiver Blick auf Unterricht vermittelt und ein moderner vernetzter Unterricht (Mathematik und Naturwissenschaften) ermöglicht werden. Das Projekt zeichnet sich dabei neben den praktischen Anteilen durch eine genuine didaktische Forschungsperspektive aus: So werden die gewonnen Unterrichtsdokumentationen dazu verwendet, um auf einer theoretischen Ebene u.a. über Interaktionsmuster (Bauersfeld 1983, Steinbring 1993, Voigt 1984, etc.), vermittelte Auffassungen (Schoenfeld 2010, Struve 1990, Törner & Grigutsch 1994), Nature of Mathematics/Science (Abd-El-Khalik & Lederman 2000, Davis & Hersh 1995, Reiners 2013) oder kognitionspsychologische Aspekte (Gopnik et al. 2010) zu reflektieren. Hierdurch wird die Praxisphase ein interessantes neues Element der Lehrerausbildung. Es ermöglicht den Studierenden praktische Erfahrungen vor dem theoretisch-reflektierenden Hintergrund wissenschaftlicher Mathematikdidaktik und liefert gleichzeitig Impulse für eine Weiterentwicklung in den beteiligten Disziplinen.

Weitere Informationen zu den übrigen Forschungsfeldern finden Sie unter den nachfolgenden Links:

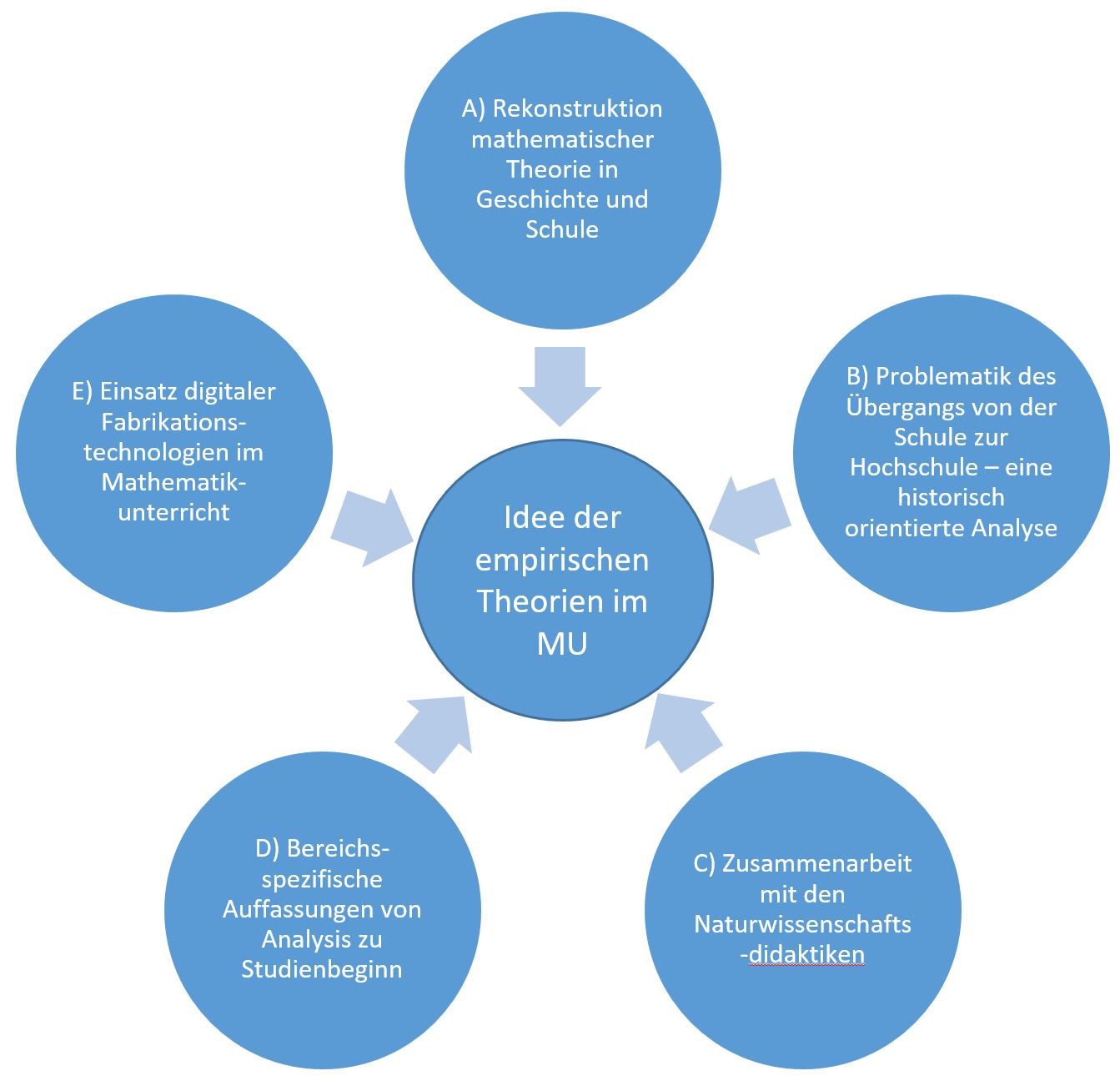
• Idee der empirischen Theorien im Mathematikunterricht
• A) Rekonstruktion der Entwicklung mathematischen Wissens in Geschichte und Schule
• B) Übergangsproblematik Schule - Hochschule
• D) Schüler/Studierendenauffassungen von Analysis
• E) MINTUS-Digital

Literatur

Abd-El-Khalick, Foyad; Lederman, Norman G. (2000): Improving Science Teachers' Conceptions of Nature of Science: A Critical Review of the Literature. In: International Journal of Science Education 22 (7), S. 665–701.

Bauersfeld, Heinrich (1983): Subjektive Erfahrungsbereiche als Grundlage einer Interaktionstheorie des Mathematiklernens und –lehrens. In: Heinrich Bauersfeld (Hg.): Lernen und Lehren von Mathematik (Untersuchungen zum Mathematikunterricht, 6), S. 1–56.

Burscheid, Hans Joachim; Struve, Horst (2010): Mathematikdidaktik in Rekonstruktionen. Ein Beitrag zu ihrer Grundlegung. Hildesheim: Franzbecker.

Davis, Philip J.; Hersh, Reuben; Marchisotto, Elena Anne (1995): The mathematical experience. Study edition. Boston, Basel: Birkhäuser.

Grigutsch, Stefan; Törner, Günter (1994): Einstellungen und Haltungen bei Studienanfängern. In: Journal für Mathematik-Didaktik 15, S. 211–251.

Philipp, Kathleen (2013): Experimentelles Denken. Theoretische und empirische Konkretisierung einer mathematischen Kompetenz. Wiesbaden: Springer (Freiburger Empirische Forschung in der Mathematikdidaktik, 1).

Reiners, Christiane S. (2013): Die Natur der Naturwissenschaften lernen zu lehren. Zum Potential eines expliziten Ansatzes. In: Michael Meyer (Hg.): Wissenschaftlichkeit und Theorieentwicklung in der Mathematikdidaktik. Festschrift anlässlich des sechzigsten Geburtstages von Horst Struve. Unter Mitarbeit von Horst Struve. Hildesheim: Franzbecker, S. 293–314.

Schoenfeld, Alan H. (1985): Mathematical Problem Solving. Orlando et al.: Academic Press.

Schoenfeld, Alan H. (2011): How We Think. In: Studies in Mathematical Thinking and Learning. New York York et al.: Routledge.

Steinbring, Heinz (1998): Mathematikdidaktik: Die Erforschung theoretischen Wissens in sozialen Kontexten des Lernens und Lehrens. In: Zentralblatt für Didaktik der Mathematik, 5, 161 – 167.

Voigt, Jörg (1984): Interaktionsmuster und Routinen im Mathematikunterricht. Theoretische Grundlagen und mikroethnographische Falluntersuchungen, Weinheim: Beltz.

Struve, Horst; (1990): Grundlagen einer Geometriedidaktik. Mannheim et al.: B I Wissenschaftsverlag

Tall, David. (2013): How Humans Learn to Think Mathematically. Exploring the three worlds of mathematics. New York: Cambridge University Press.