Wie kann eine Kombination von mathematischer und visueller Ästhetik gelingen?

Rechenmandalas

Rechenmandalas oder auch "bunte Hunde" sind ein beliebtes Format der Rechenübungen in der Grundschule, die als spielerisches Aufgabenformat die "grauen Päckchen" ersetzen sollen. Das Rechnen wird bei diesem Übungsformat mit dem Ausmalen eines Bildes begleitet und soll das Lernen der SchülerInnen abwechslungsreicher und spielerischer gestalten. Jedes Feld im Mandala erhält eine Rechenaufgabe und je nach Ergebnis muss dieses ausgemalt werden. Die entstehenden Muster gelten als Selbstkontrolle, sodass die Lernenden an Hand der Farben überprüfen können, ob sie richtig gerechnet haben.  Es stellt sich jedoch die Frage, ob diese Rechenmandalas genau wie die „schönen Päckchen“ tatsächlich „schön“ sind oder nur eine äußerliche ästhetische Schönheit
vorweisen. Die Beantwortung dieser Frage ist ganz leicht, denn das fertige Endprodukt eines Rechenmandalas ist zwar schön anzusehen, jedoch hat diese Schönheit nichts mit den Kriterien mathematischer Ästhetik zutun.

„Der Schüler wird bei dieser Methode dazu erleitet, sich auf Äußerlichkeiten zu konzentrieren. Denken und Rechnen werden
entkoppelt.", so Wittmann. Es besteht beispielsweise die Gefahr eines vorhersehbaren Ausmalens, sodass das Rechnen in den  Hintergrund und ein stumpfes Anmalen in den ordergrund tritt. Wenn zum Beispiel drei von vier Sternen innerhalb eines Mandalas gelb angemalt werden müssen, ist die Wahrscheinlichkeit, dass der vierte Stern ebenfalls gelb sein soll sehr hoch. Die SchülerInnen werden dadurch dazu verleitet, die Aufgabe gar nicht erst zu rechnen und direkt den Stern anmalen. Auch fehlen die Zusammenhänge der einzelnen Rechenübungen zueinander. Bei den „schönen Päckchen“ herrscht zwischen den  einzelnen Aufgaben eines Päckchens eine bestimmte Verbindung, die der Lernende während dem Rechnen begreift und ein Verständnis für den vorliegenden Zusammenhang entwickelt. Bei dem Format der Rechenmandalas sind diese Bezüge nicht ersichtlich.
Daraus resultiert demnach die Frage, ob sich beides - eine visuelle und eine mathematisch arithmetische Schönheit – verbinden lässt.

Zunächst ist es wichtig, dass das Anmalen beispielweise nicht zu regelmäßig ist und die SchülerInnen immer noch rechnen müssen. Bleiben wir bei dem Format der Rechenmandalas, so ließe sich das zuvor geschilderte Aufgabenformat umkehren. Es wird demnach kein fertiges Mandala, welches an Hand der Aufgaben ausgemalt werden muss, vorgegeben, sondern die SchülerInnen erhalten ein leeres Mandala, welches sie mit eigenen Aufgaben füllen müssen. Hierbei müssen die Kinder selbst durch experimentieren und
ausprobieren Zusammenhänge zwischen den einzelnen auszumalenden Feldern sowie den selbst ausgedachten Aufgaben herstellen. Sie würden eigene schöne Päckchen erstellen, diese in das leere Mandala eintragen und dann deren Zusammenhang mit einer Farbe
deutlich machen. Hier könnten den SchülerInnen auch ein Mandala vorgelegt werden, in dem teilweise Flächen freigelassen und / oder bereits angemalt sind.

Arbeitsmaterial für die Jgst. 2/3:

Ein wirklich schönes Rechenmandala

 

Durch visuelle Elemente mathematische Schönheit sichtbar machen

Eine weitere andere Möglichkeit Aufgaben schön darzustellen beziehungsweise visuell zu unterstützen ist beispielweise Vorgänge innerhalb eines Entdeckerpäckchens farblich zu  verdeutlichen sowie erklären zu lassen, was genau bei den hervorgehobenen Zahlen
geschieht. Die gleichen Ergebnisse aber auch die Zusammenhänge der einzelnen Aufgaben zueinander werden auf diese Art und Weise von den SchülerInnen erkannt.

Bei diesem Rechenformat können die Lernenden eigene strukturgleiche Aufgaben erstellen und diese weiterführen.
Auch das Experimentieren mit Rechenketten, bei dem mit dem Ergebnis weitergerechnet werden soll, zeugt von einer gewissen Ästhetik, denn einzelne Rechenketten können auf eine bestimmte Arte und Weise miteinander verbunden werden.

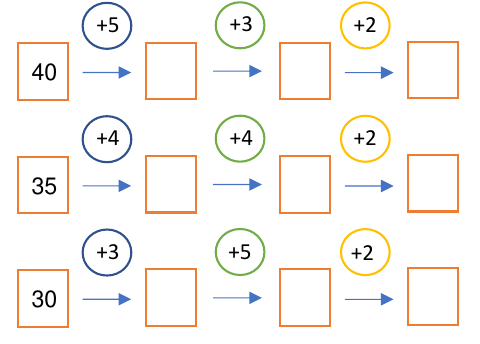
Auch das Experimentieren mit Rechenketten, bei dem mit dem Ergebnis weitergerechnet werden soll, zeugt von einer gewissen Ästhetik, denn einzelne Rechenketten können auf eine bestimmte Arte und Weise miteinander verbunden werden.

Bei dieser Aufgabe stellt sich beispielsweise die Frage, inwieweit diese Rechenketten zusammenhängen. Die Gemeinsamkeiten,
Unterschiede und Veränderungen sollen farblich markiert und somit verdeutlich werden. Solche Ketten können die
SchülerInnen selbst erstellen oder auch weiterführen.

Ob die beiden zuletzt vorgestellten Aufgabenformate für Kinder die gleiche offensichtliche
Ästhetik aufweisen wie Rechenmandalas ist jedoch unklar.

Es stellt sich abschließend die Frage, ob geometrische Gebilde, wie etwa Mandalas (Parkette, Kreisfiguren) immer rein ästhetisch sind und wie die Schönheit geometrischer Objekte begründet wird. Es lässt sich sagen, dass eine bestimmte Regelmäßigkeit ein größeres visuelles Vergnügen hervorruft, jedoch auch deutlich wird, dass ein zu hohes Gleichmaß ebenfalls eintönig ist. Geometrische Regelmäßigkeiten, die durch andere regelmäßige Objekte unterbrochen werden sind ebenfalls visuell schön. Es ist jedoch
wichtig, dass die jeweiligen Strukturen erfasst werden.

 

 

Quelle: E. Wittmann. Wider die Flut der „bunten Hunde“ und der „grauen Päckchen“: Die Konzeption des aktiv-
entdeckenden Lernens und des produktiven Übens. In: E. Wittmann, G. N. Müller, Handbuch produktiver
Rechenübungen. Vom Einspluseins zum Einmaleins. Band 1, S. 157-171.

Text und Arbeitsmaterial:  Kristina Sickinger