Ästhetik und Problemlösen
Die mathematische Erfindung im Unterricht
Poincare trifft Polya und die Rolle des Ästhetischen
Die zentrale Rolle des Ästhetischen in mathematischer
Erfindung und Problemlöseprozessen
Zeit für unbewusste Arbeit und ästhetisches Gefühl
Abgeleitete Unterrichtsprinzipien für einen problemlösenden, die Ästhetik berücksichtigenden Unterricht:
Aus den Beobachtungen zur mathematischen Erfindung, dem Problemlöseprozess und den Rollen des Ästhetischen lassen sich Folgerungen für die Gestaltung des Mathematikunterrichts ableiten. Grundlegend sollte die Unterrichtsstruktur so angepasst werden, dass die Schülerinnen und Schüler die drei Phasen durchlaufen können. Um dies zu ermöglichen müssen verschiedene Aspekte berücksichtigt werden. Für den Einstieg bedeutet dies, dass die Kinder überlegen, ob sie bekannte oder verwandte Aufgaben kennen, die sie mit der neuen Aufgabe in Beziehung setzen können. So kann die Aufgabe verstanden werden und die Schülerinnen und Schüler können sich überlegen, wie sie die Aufgabe lösen möchten. Zudem sollte die Aufgabe so gewählt werden, dass die Kinder sich ihr über verschiedene Zugänge nähern können. So kann jedes Kind eigene Lösungsstrategien entwickeln, wobei es nach eigenen Fähigkeiten und Vorlieben arbeiten kann. Bei dem Abschluss des Unterrichts spielt die Evaluation eine große Rolle. Hier geht es darum, sich über die Lösungswege auszutauschen. Dabei reflektieren die Schülerinnen und Schüler sowohl ihren eigenen als auch den Lösungsprozess der anderen Kinder. Wichtig ist hierbei, dass die intuitive bzw. ästhetische Wahl eines Bearbeitungsweges als legitim und mathematisch angesehen wird.
Da die unbewusste Phase nicht gesteuert werden kann und es vorkommen kann, dass die Schülerinnen und Schüler erst in einer anderen Schulstunde oder gar nach der Schulzeit eine Lösungsidee entwickeln, ergeben sich aus diesem Aspekt weitere Konsequenzen. Zum einen sollte der Stand der Arbeit nach der bewussten Einstiegsphase gesichert werden, beispielsweise in einem Lösungstagebuch. So kann später auf diese Aufzeichnungen zurückgegriffen werden und sie können verarbeitet werden. Zum anderen sollte der Austausch der Aufgabenlösung zeitlich versetzt erfolgen, um die Schülerinnen und Schüler nicht an ihrer mathematischen Erfindung zu hindern. Denn wenn die Kinder die Lösungswege und somit die Lösung der Aufgabe von ihren Mitschülerinnen und Mitschülern vorgestellt bekommen, stehen diese den individuellen Ideen der übrigen Schülerinnen und Schüler im Weg.
Um einen problemlösenden Unterricht noch mehr zu ermöglichen und die Chance auf kreative Ergebnisse in der unbewussten Phase zu verstärken, müsste an den Schulen sehr freies Arbeiten zur Kultur werden. Damit ist gemeint, dass die Fächerstrukturen bzw. die Strukturen der Schule so aufgebrochen werden, dass die Kinder sich jederzeit selbst überlegen, was sie gerade bearbeiten und auch zwischen den Arbeiten wechseln können.
Es zeigt sich, dass neben größeren strukturellen Veränderungen auch schon kleine Anpassungen des Unterrichts zu einem problemlösenden, die Ästhetik berücksichtigenden Mathematikunterricht führen können.
Zahlenmauern für Profis
Beispielhafter Unterrichtsverlauf für einen problemlösenden, die Ästhetik berücksichtigenden Unterricht
Klasse: 2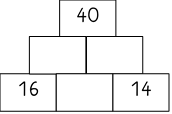
Arbeitsmaterial: Zahlenmauern für Profis
Tag 1 | |||
Phase | Unterrichtsaktivität Lehrperson | Unterrichtsaktivität Schüler | Begründung |
Einstieg | Lehrperson präsentiert eine besondere Zahlenmauer siehe Bild oben Fragen: Hast du so eine Aufgabe vorher schon gesehen? Hast du dieselbe Aufgabe in einer etwas anderen Art gesehen? Kennst du eine ähnliche Aufgabe? (falls keine Erklärung einer „normalen“ Zahlenmauer der SuS kommt, erfolgt dies von der Lehrperson)
Wie können wir unsere spezielle Zahlenmauer füllen? Was ist unbekannt? Was ist gegeben? Wie lautet die Bedingung? => Problemstellung (Aufgabe wird nicht gemeinsam gelöst!) | SuS sitzen im Halbkreis (Richtung Lehrperson)
Ggf. Erklärung / Präsentation von einer „normalen“ Zahlenmauer | Die SuS werden mit der Problemstellung konfrontiert (hier die besondere Zahlenmauer)
Das Vorwissen der SuS wird aktiviert. Durch das Fragen nach bekannten Aufgaben wird der Aufgabentyp Zahlenmauer erklärt. |
Arbeitsphase | Lehrperson hilft, wenn SuS Verständnisprobleme haben | SuS bearbeiten in Einzelarbeit ein Arbeitsblatt (siehe unten), auf dem sie das Problem lösen sollen
| Durch die Einzelarbeit kann jedes Kind sich in seinem Tempo und auf seinem Weg zur Lösung kommen. SuS können ausprobieren oder systematisch entdeckend vorgehen. |
Offenes Ende | | Schnelle SuS können sich eigene besondere Zahlenmauern ausdenken. | Keine Auflösung der Aufgabe, damit alle Kinder die Chance haben, eine Strategie zu entwickeln. |
Tag 2 | |||
Phase | Unterrichtsaktivität Lehrperson | Unterrichtsaktivität SuS | Begründung |
Einstieg | | SuS stellen die Problematik vom vorherigen Tag vor. | Die Erinnerungen an das Thema werden geweckt. |
Arbeitsphase | Lehrkraft leitet die Aufgabe an; teilt die Kinder in Gruppen ein (ca. vier Kinder pro Gruppe)
Frage: Könnt ihr erklären, wie ihr durch Überlegen die Zahlenmauern füllen könnt?
| SuS tauschen sich in Mathekonferenzen über ihre Lösungswege aus.
SuS tauschen sich in ihrer Gruppe zu der Frage aus und erstellen ein Plakat zu ihren Strategien. | Beantwortung der Fragen: Was ist wichtig an meiner Strategie? Was habe ich gut gemacht? Wie haben andere Kinder das Problem gelöst?
|
Schluss |
Welchen Lösungsweg findest du schöner? Welcher Lösungsweg gefällt dir am besten? Warum? | Freiwillige SuS stellen ihre Gruppenplakate vor.
Sitzkreis: Gesprächsrunde | SuS tauschen sich gemeinsam über ihre Strategien und Denkweisen aus. Austausch über ästhetische Kriterien |
Text und Arbeitsmaterial von Celina Göbel
